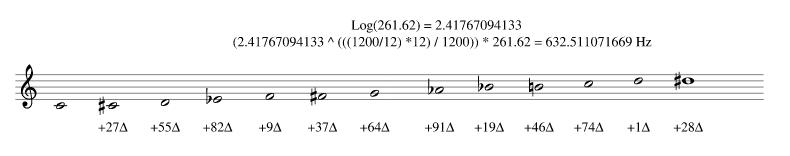Dialógica Sonoiética
Por una combinatoria de la X va o la 8 va modificada ⇒
Apuntes para un curso imaginario
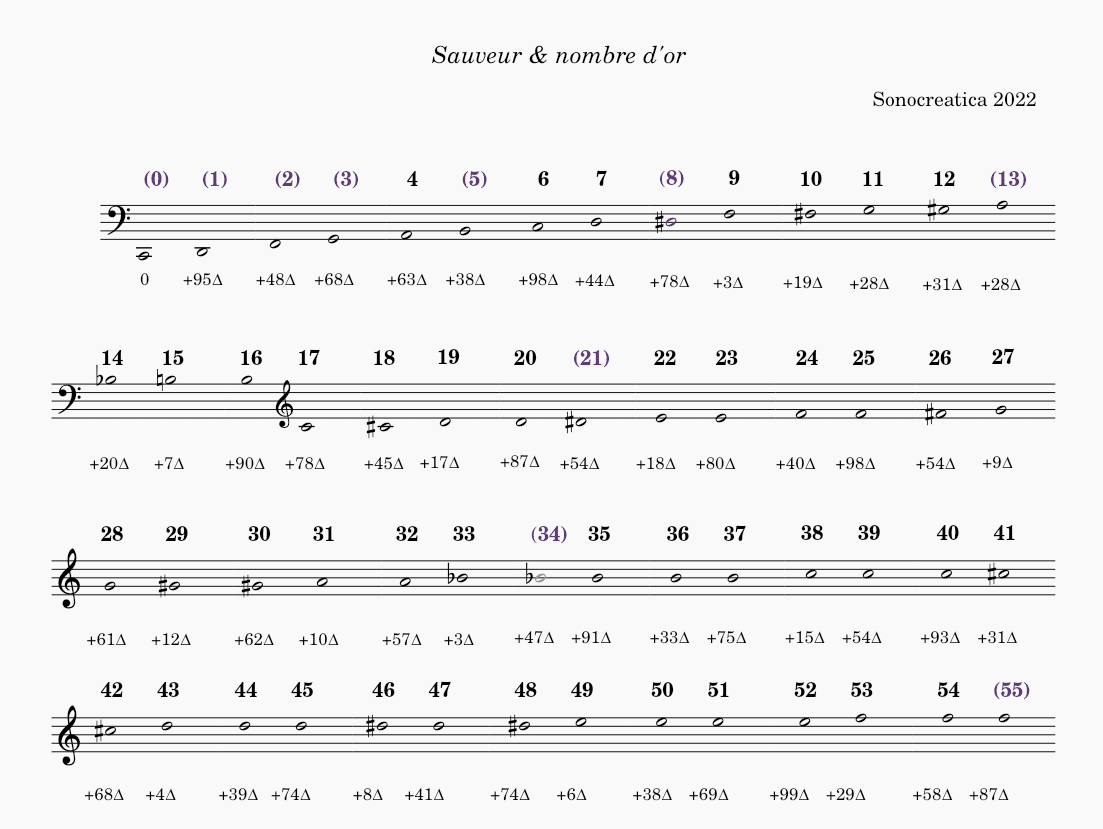
Ma fin est mon commencement …
Lectura preliminar⇒
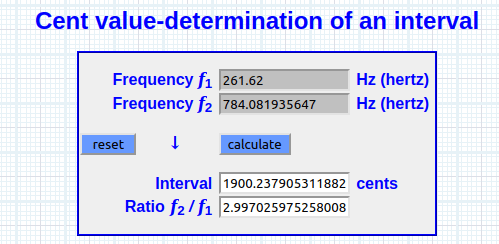
2^ (1/12) × 261.62 = 1 semitono / 2^ (12/12) × 261.62 = 8va
…Y dado que el producto del límite logarítmico de la 8va (a saber, 2) consigue su fuente en el logaritmo de 100 Log(100) = 2
Sea: log(100) * 261.62 [C4] = 8va [C5]
Procedamos entonces a indagar otras formas globales de recorridos espaciales subyacentes
PROBLEMÁTICA:
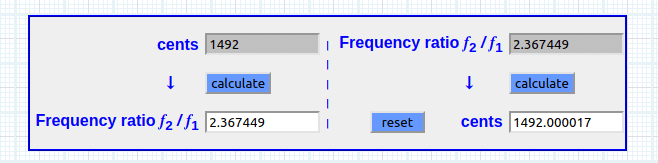
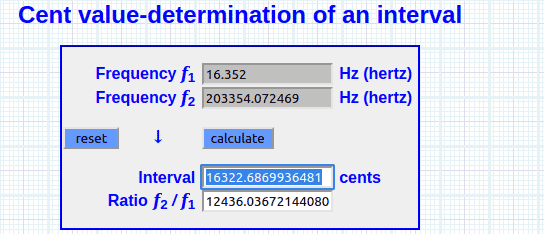
(A) Supongamos una “equisava (abreviación Xva ) de 1492 cents (∆)
(B) Sobre una clausura operacional “espacial a operar de 1200 (∆)
I. 2 ^ (1492 ÷ 1200) 2.3674489771 resultado equivalente (~) al producto del índice logarítmico PIL o límite (* )
Sea, log(100)^(1492 ÷ 1200) 2.36744897718 (PIL )
Se lee , log de 100 elevado a la potencia de una Xva , dividida entre una 8va temperada e
igual al producto del índice logarítmico
log(100) ^ ( Xva ÷ 8va ) = PIL
Formulación abierta
{ B( log) ^ ( Xva ÷ 8va ) } = PIL
Luego
II. Producto (PIL
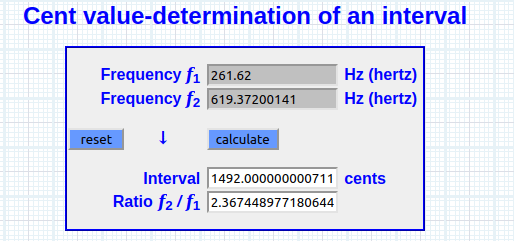
PIL × f(sb) = Xva
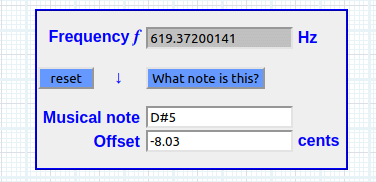
2.36744897718 × 261.62 = 619.37200141 Hz ~ Xva , o “ frontera flotante frecuencial” y equivalente a un primer ciclo de proliferación.
…y así sucesivamente…
Verificación externa
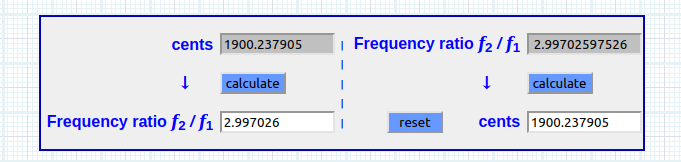
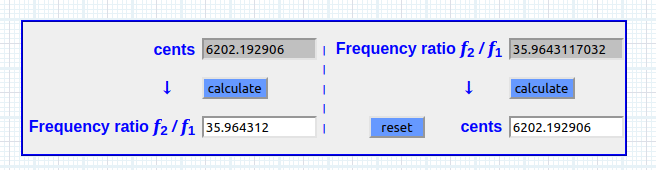
Ratio f2 / f1 ~ PIL
Recursividad log(100)^(1492 ÷ 1200) = 2.36744897718
Algunos ciclos residuales
Sea, 261.62 × 2.36744897718 D5 + 92 (∆)] ascendente…
619.37200141 ÷ 2 D4 + 92 (∆)] descendente …
Tendremos entonces :
619.37200141 x 2 = 1238.74400282 Hz [D6 + 92]
619.37200141 x 3 = 1858.11600423 Hz [A6 + 94 (∆) ]
619.37200141 x 4 = 2477.48800564 Hz [D#7 +92 (∆) ]
Recordatorio
[Log(100) = 2] límite logarítmico de la 8va equivalente a 1200 (∆)
100 cents = mínima del conjunto temperado cromático (1 semitono)
Obtenemos así:
1492 ÷ 100 = 14.92
14.92 – 12 = 2.92 (200 + 92 cents)
Sea una 8va + 292 cents = 619.37200141 Hz
Aún más proliferante
Una variante con desplazamiento de la frontera flotante inicia l
(La frecuencia logarítmica)
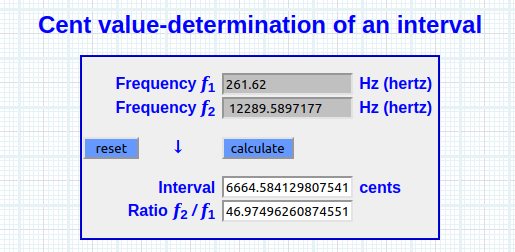
Log(261.62) ^ (1492 ÷ 1200) × 261.62 784.081935647 Hz [G5]
Sea , una 8va + 700 (∆)
Log(261.62) ^ (1492 ÷ 1200) 2.99702597526 [PIL
Verificación externa
Proliferación de ciclos de tesitura ( Xvas u 8vas modificadas)
Log(261.62) 2.41763773965
2.41767094133 ^ (1492÷1200) 2.99702597526 ~ PIL
Verificación externa
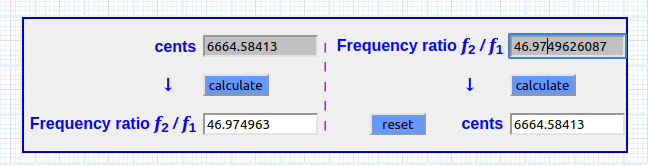
2.99702597526 ^ (1492÷1200) × 12 = 46.9749626087 PIL
Verificación externa
46.9749626087 × 261.62 = 12289.5897177 Hz [F#9+65 cents]
Verificación externa
2.41767094133 ^ (1492 ÷ 1200) ×12 35.9643117032 PIL
35.9643117032 ^ (1492 ÷ 1200) × 261.62
Verificación externa
Formulación sonopoiética
Aditivo
B(e) ^ (((Ep ÷ mod) × d) ÷ Ea)) × f ° = ms (en base 2)
Corolario
Dado un espacio frecuencial (Hz-Cents) de recorrido “n” (Octava o Equisava e incluso, magnitud de una constante; procederemos en un primer tiempo a la operación divisiva entre la 8va, (X)ava o constante deseadas y un valor mínimo que habremos de fijar en 100 cents (~ 1 semitono).
Seguidamente, el producto obtenido lo adicionamos a la cifra 12 : correspondiente al conjunto cromático del recorrido total que se desea transformar (la 8va ~ 1200 cents).
{ (2^((((1492 / 1200) * 1200) / 1200)) * 261.62 }
(2^(((1492 / 1200) * 1200) / 1200)) = 2.36744897718 [PIL
{((1200 × log( 619.37200141 ÷ 261.62)) ÷ log (2)) ÷ 24
{((1200 × log( 619.37200141 ÷ 261.62)) ÷ log (2)) ÷ 24 × 24
((1200 × log( 619.37200141 ÷ 261.62)) ÷ log (2))
Frecuencia substrato dividida entre el valor mínimo octavante
261.62 ÷ 100 = 2.6162 [PIL
(261.62 ÷ 100) × 261.62 = 684.450244 Hz [E5 + 65 (∆)]
Ossia
((1200 × log( 684.450244 ÷ 261.62)) ÷ log (2)) = 1664.96740129 (∆)
Origen
(261.62 ÷ 100)^(((1200 / 1200) * 1200) / 1200)) 2.6162 [PIL]
Extensionalidad
(261.62 ÷ 100)^(((1200 / 1200) * 1200) / 1200)) × 261.62
Así, una vez definida las variables para el operar, se abre la posibilidad de modelizar y formalizar cualquiera constante escalística, frontera flotante o base frecuencial logarítmica, etc
En nuestro proceder dialógico todos los operadores aritméticos básicos, pueden ser empleados. No obstante, el sentido de los resultados (por ser absolutos), necesitan de la valoración de un vertimiento semántico o significación de lo deseado.
Log(1492) = 3.17376882314 PIL
(3.17376882314^(((1492 / 1492) * 1200) / 1200)) * 261.62 = 830.32139951 Hz [G5 + 41 ∆]
(3.17376882314^(((1492 / 1492) * 1492) / 1200)) * 261.62 = 1099.75569114 Hz [G6 + 86 ∆]
Nuestra Xva
Otro ejemplo
VÍNCULOS DE UTILIDAD PROCESUAL
Operadores y operandos
Operadores y Operandos B
https://desarrolloweb.com/articulos/2165.php
Formulación con constante (K) evolutiva
Segmento ((k × e) ÷ mod)…
e = término escalístico
(nuestra formulación) B(e) ^ (((Ep ÷ mod) × d) ÷ Ea)) × f ° = ms
(2^(((50 × 1/ 1200) * 1492) / 1200)) * 261.62
Verificación
{((1200 × log( 619.37200141 ÷ 261.62)) ÷ log (2)) ÷ 24
{((1200 × log( 619.37200141 ÷ 261.62)) ÷ log (2)) ÷ 24 × 24
{(2^(((50 × 24/ 1200) * 1492) / 1200)) [D5+92] }
Simetría infra-frecuencial metatonal
((1200 × log( 619.37200141 ÷ 261.62)) ÷ log (2)) ÷ 24 × 24) / 2
(2^(((746/ 1200) * 1492) / 1200)) * 261.62
(antípoda o frecuencia ausente estructurante)
sea un recorrido de 928 (∆)
conjunto residual
928 ÷ 28 = 33.1428571429
28 ÷ 4
(2^(((746/ 1200) * 1492) / 1200)) = 1.70874709944 PIL
261.62 × 1.70874709944
Operación sobre 1200
(2^(((746/ 1200) * 1200) / 1200)) × 261.62
(2^(((746/ 1200) * 1200) / 1200))
1.53865167506 × 261.62
Recordatorio
log(100)^(1492 ÷ 1200) 2.36744897718 (PIL)
Retorno a la frecuencia substrato
{2^((((1492 / 14.92) * 12) / 1200)) * 261.62
Proliferación y recursividad
Logaritmo del producto obtenido :
Log(619.37200141) 2.79195156927 ⇒ ( PIL * 261.62)
Sea un 8va + 578 cents = 1 cuarta + 78 (∆) |
A la búsqueda de una tesitura endógena :
2.79195156927 × 14.92 41.6559174135
Procedimiento
Acoplamiento
261.62 × 41.6559174135
Verificación de savarts
4 × 1610.75 = 6443
6443 ÷ 1610.75
A propósito del savart
Recordatorio
1000 × log10(523.24 ÷ 261.63 redondeados a 1200 ÷ 4 = 300 pasos dentro de una Xva
Sea (nuestra modelización)
((log(1200) * log(523.24 / 261.62) / log(1200) * 1000 301.029995664
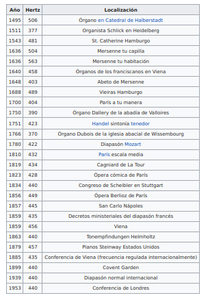
A propósito del Sauveur fuente
véase también
DIDACTOLOGÍA
DECONSTRUCCIÓN 1492
una definición
I. 2 ^ (1492 ÷ 1200) × 261.62
II. 1200 × log( 619.37200141 ÷ 261.62) ÷ log (2)
/////////////////////////
BIFURCACIÓN [■] Y PROLIFERACIÓN 1942
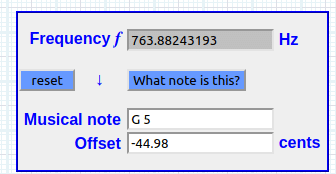
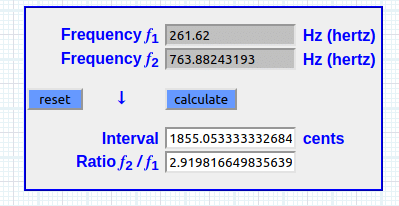
III. Log(261.62) 2.41767094133
IV. 2.41767094133 × 261.62 632.51101671 Hz
V. 1200 × log(632.511071671 ÷ 261.62) ÷ log (2) 1528.34147881 cents
VI. Log(261.62) × 261.62
/////////////////////////
BIFURCACIÓN [■] Y PROLIFERACIÓN 1942
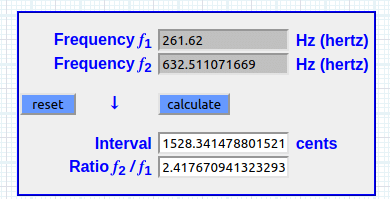
VII. Log(261.62) 2.41767094133
VIII. 2.41767094133 × 261.62 = 632.511071671 Hz
IX. 1200 × log(632.511071671 ÷ 261.62) ÷ log (2) = 1528.34147881 cents
X. Log(261.62) × 261.62 = 632.511071669 Hz
/////////////////////////
“1492” Hibridación, equipartición y bifurcación frecuenciales
XI. 1/4 de 1492 :
(2^(((50 × 1/ 1200) * 1492) / 1200)) * 261.62 = 271.18518962 [C4 + 62 (∆)]
(2^(((50 × 24/ 1200) * 1492) / 1200)) * 261.62 = 619.37200141 Hz [D5+92]
Ídem
A. 1/3 de 1492 [ ÷ 18] ~ (1492 ÷ 18) = 82.8888888889 (∆)
(2^(((83 × 1/ 1200) * 1492) / 1200))
OSSIA
(2^((((1492 ÷ 18) × 1/ 1200) * 1492) / 1200)) * 261.62
(2^(((83 × 18/ 1200) * 1492) / 1200)) * 261.62
B. 1/5 ” ” [ ÷ 30] ~ (1492 ÷ 30)
C. 1/7 ” ” [ ÷ 42] ~ (1492 ÷ 42)
D. 1/9 ” ” [ ÷ 54] ~ (1492 ÷ 54)
E. 1/11 ” ” [ ÷ 66] ~ (1492 ÷ 66)
F. 1/12 ” ” [ ÷ 72] ~ (1492 ÷ 72)
Espacialización de la equipartición frecuencial
Sobre una tesitura de 14 octavas temperadas
Sea: (1200×14) = 16800 (∆)
Ejemplo:
(16800 ÷ 1492) × 72
(16800 ÷ 1492) = 11.2600536193 (11 [X]vas + 260 )
/////////////////////////
Peroratio
(2^(((1492 / 1200) * 1200) / 1200)) * 261,62
Recursividad (2^(((1492 / 1200) * 1200) / 1492)) * 261,62
Retorno a la 8va temperada
((1492 * log((523.24 / 261.62))) / log(2) / (1492/100) * 12
1492 / 100 = 14.92 (términos)
((14.92/ 12) * 1200) / 14.92
Aditivo
(1/12) × 1492 = 124.333333333 [1/2] K
Ó
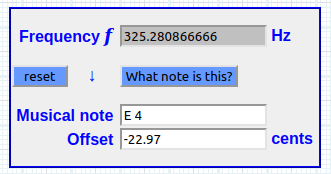
1492 ÷ 1200 = 1.24333333333 ratio o PIL * 261.62 Hz)
sea: 325.280866666 Hz
(1492 ÷ 1200) × 100 = 124.333333333
Yuxtaposición espacial logarítmica multiplicativa
Log(1492) * Log(1200) * 261.62 = 2556.71008156 Hz ~ 3946.492602914504 o 3947 cents
ACERCA DE LA CIFRA 1492
/////////////////////////
Recuerdos del pasado/presente/futuro…
(1/24) × 1200 =
(1/18) × 1200 =
(1/30) × 1200 =
(1/72) × 1200 =
Corolario ((1200 × 12) ÷ 72) ÷ 12
Primer segmento (×) / [14400] 12 octavas
Segundo segmento (÷) / [200] 1 tono
Tercer segmento (÷) / [16.6666666667] 1 doceavo de tono
Procedencia: L’héritage de Wyschnégradsky
/////////////////////////
Modo natural simétrico infra-tonal ⊙ Doble división cuaternaria de la 8va
en el concepto metatonal
https://sonocreatica.org/wp-content/uploads/2022/06/Modo-symetrique-infratonal-1.ogg
1200 ÷ 8 = 150 (ocho pasos)
(2^(((1200/ 8) * 1) / 1200)) * 261.62 = 285.29863302 (Db + 50 cents) 3/4 de tono
(2^(((1200/ 8) * 8) / 1200)) * 261.62 = 523.24 ( 8va )
/////////////////////////
Corolario aritmético para el veinticuatroavo de 8va :
1200 ÷ 24 = 50 cts | 2 ^ (50÷1200) × 261.62 Hz 269.286051151 Hz |
| 2 ^ (50 ÷ 1200) = 1.02930223664
Fuente 1
Fuente 2
Curiosidades
Sectio Aurea
log(1618)^(((1618 / 1200) * (1618 ÷ 21 × 1)) / 1200) × 261.62 = 289.406250346 Hz [C+175 cents]
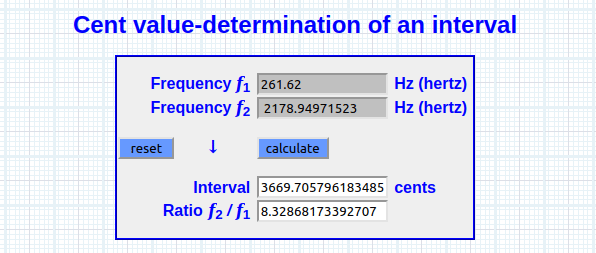
log(1618)^(((1618 / 1200) * (1618 ÷ 21 × 21)) / 1200) × 261.62 =
2178.94971523 Hz [C7+70 cents]
log(1618)^(((1618 / 1200) * (1618 ÷ 21 × 21)) / 1200) = 8.32868173391 [PIL
LUDUS
Hibridación con amplificación de la tesitura
(1200 log(2179 / 261.62)) / log(2) = 3669.74574832 cents
Verificación
3669.74574832 ÷ 21 = 174.749797539 cents redondeado a [C+175 cents]
Extensionalidad
(1618 × log(2179 / 261.62)) / log(2)
4948.04051732 ÷ 21
Límite logarítmico (PIL)
Log(1618)^(((1618 / 1200) 4.81671830595 PIL (1618 ÷ 21 × 21)) / 1200) 1.34833333333 PIL Log(4948.04051732) 3.69443324722 PIL
Recordatorio
En nuestro procedimiento dialógico todos los operadores aritméticos básicos, pueden ser empleados. No obstante el sentido de los resultados (por ser absolutos), necesitan de la valoración de un vertimiento semántico o significación de lo deseado [ ¿*?]
Experiencia sonora: Fibon(ave) fibonéchelles
Intuición de un espacio
reducción eidética
semejante a una enacción
Primera intuición
Una distancia, magnitud o constante de 21 vibraciones sobre un recorrido contiguo de 144 pasos.
Sea entonces: 21 × 144 = 3024
2. Una vez aceptado el valor de cálculo (cent), anexamos el producto obtenido al operador
Segunda intuición
Búsqueda de una asociación con el universo frecuencial en hercios Formulación
Mínima: 261,62*(2^(((3024/144)*1)/1200/1)) 264.812795672 Hz (C4+21 cents)
Frontera flotante: 261,62*(2^(((3024/144)*144)/1200/1)) 1500.60548794
Vínculos para la verificación :
https://newt.phys.unsw.edu.au/music/note/
http://www.sengpielaudio.com/calculator-centsratio.htm
Hyperphysics
Recursividad
((1200 log (1500.60548794/261.62) / log(2))
((1200 log (1500.60548794/261.62) / log(2))÷144
Nuevo parámetro:
Espacio intuido
144×144
equivalente a la multiplicación de la constante por los pasos contiguos.
Formalización
261,62*(2^(((20736/144)*1)/1200/1))
261,62*(2^(((20736/144)*1)/20736/144))
Recordatorio
… Toda transformación, supone la presencia de lo que se desea transforma r :
261.62 * (2^(((20736 / 207.36) * 12) / 1200))
A ese propósito, el enunciado preliminar de Félix Guattari (en su texto La hétérogènese machinique la máquina precede a la técnica y no lo contrario.
Deducimos entonces —que una formulación es la condición previa al cálculo que deseamos efectuar.
Lectura recomendada
Preámbulo
Octava (2^1)
261.62 * (2 ^ 1)
log(523.24 / 261.62)
0.30102999566 * 1000
Log(2)
Log(100)
Xva (1492): 261.62 * (2.3674489771^1)
Desarrollo
Así, el concepto Guattariano de máquina, enactaría de prime abord la noción de “consistencia de enunciación específica”.
Lectura refrescante
Nuestra formulación (algunos ejemplos)
… la presencia de lo que se desea transforma r
B(e) ^ (((Ep ÷ mod f ° = ms (en base X) |comentario |
log(100)^(((1200 / 1200 ) * (1200 ÷ 12 × 12)) / 1200) × 261.62
[C5] 8 va
Producto índice logarítmico (PIL
(log(1618)^(((1618 / 1200 ) * (1618÷21×21)) / 1200) × 261.62 = 2178.94971523 Hz
[C#6 + 70 (∆)]
Producto índice logarítmico (PIL 8.328681733919
Verificación externa
Ratio f2 / f1 ~ PIL
Recursividad
261.62 × (8.32868173392707 ^ 1) 2178.94971523 Hz
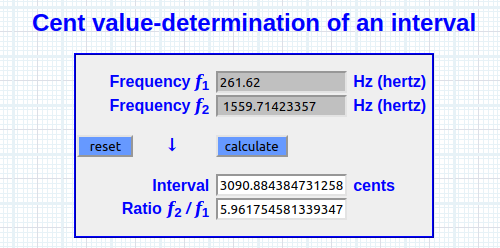
(log(1492)^(((1492 / 1200 ) * (1492÷21×21)) / 1200) × 261.62 = 1559.71423357 Hz
[G5 + 91 cents]
Producto índice logarítmico (PIL 5.961754581347
Ratio f 2 / f 1 ~ PIL
Recursividad
261.62 × (5.961754581347^1) = 1559.71423357 Hz
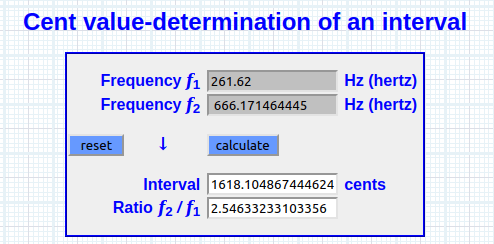
(log(1100)^(((1100 / 1200 ) * (1100÷11×11)) / 1200) × 261.62 = 666.171464445
[E5 + 18 cents]
Producto índice logarítmico (PIL 2.54633233103
Ratio f 2 / f 1 ~ PIL
Recursividad
261.62 × (2.54633233103356^1) = 666.171464445 Hz
Coda
En fin, dado que el producto del límite logarítmico de la 8va (a saber 2) consigue su fuente en el logaritmo de 100, la logaritmización sistemática de la base espacial operada podría revelarnos la existencia (al menos) de 4 variantes endógenas con sus respectivas fronteras flotantes.
B(e) ^ (((Ep ÷ mod) × d) ÷ Ea)) × f ° = ms
A. Log (100) ^ (1492 ÷ 1200) × 261.62
log(100)^(1492 ÷ 1200) 2.36744897718 PIL
B. Log (261.62) ^ (1492 ÷ 1200) × 261.62
Log (261.62) ^ (1492 ÷ 1200) 2.99702597526 PIL
C. Log (1492) ^ (1492 ÷ 1200) × 261.62
log (1492) ^ (1492 ÷ 1200 )4.20363768496 PIL
D. Log (1200) ^ (1492 ÷ 1200) × 261.62
Log (1200) ^ (1492 ÷ 1200) 4.04844115625 PIL
Origen especulativo : despliegue de una frecuencia proliferante
(log 261.62^(((1200 / 12) * 1) / 1200)) * 261.62
Audio
Otro ejemplo en MuseScore
(log 261.62^(((1200/12) * 12)/1200)) * 261.62 = 632.511071669 [Eb5+28 cents]
Cálculo, sonopoiésis & movimiento (el objeto en su recorrido)
Sobre pensamiento logarítmico
Recreaciones
Génesis del cálculo sonopoiético
Aclaratoria
Deseamos informar a nuestros amables lectores que el empleo de las operaciones aritméticas expuestas en la presente publicación, al igual que otras semejantes, existentes en diferentes lugares de nuestro porta lposeen un fundamento esencialmente creativo y obedecen al desarrollo de un “constructo metodológico” en aras de una invención musical.
Lecturas adicionales
Heinrich Rudolf Hertz
El cuaderno abierto 2019
El cuaderno abierto 2020
Hans-Georg Gadamer
EL ELEMENTO LÚDICO DEL ARTE
1990-2002 | Verdad y Método I / II fuente | Sonocreatica Lexicon
Orígenes de nuestra preocupación (cal)






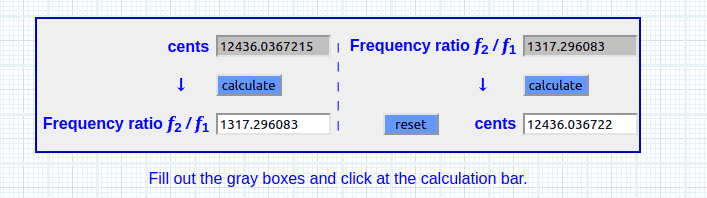
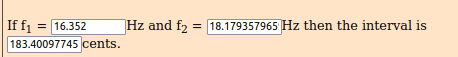
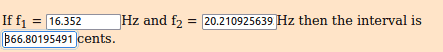
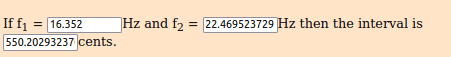
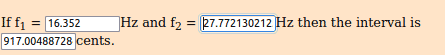
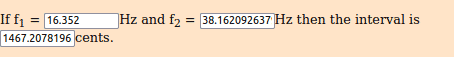
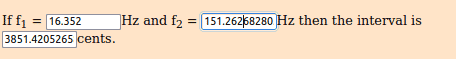
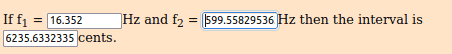
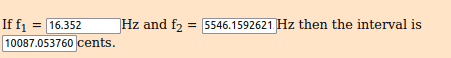
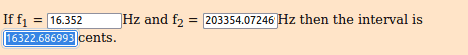

 Ratio f2 / f1 ~
Ratio f2 / f1 ~