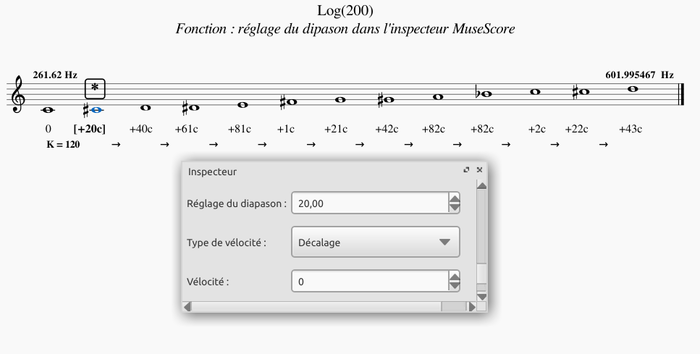
Quelques exemples dans l’emploi de la formule du postulat :
B(e) ^ (((Ep ÷ mod) × d) ÷ Ea)) × f° = ms (en base 2)
segment (Ep ÷ mod]
(1/1200) ∼ 1 centième de ton (cent) [1200 termes] C4 + 1 cent
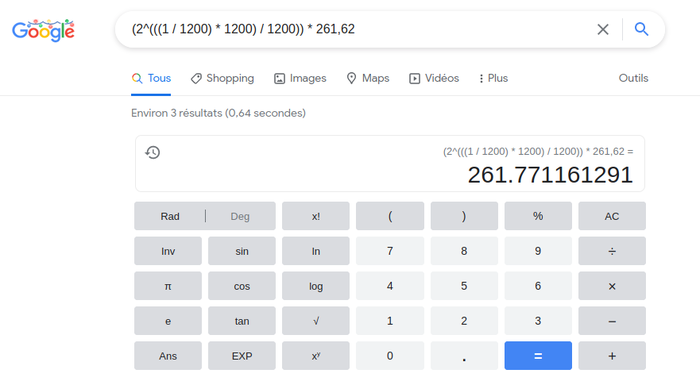
(50/1200) 1/4 de ton [24 sons] C4 + 50 cents
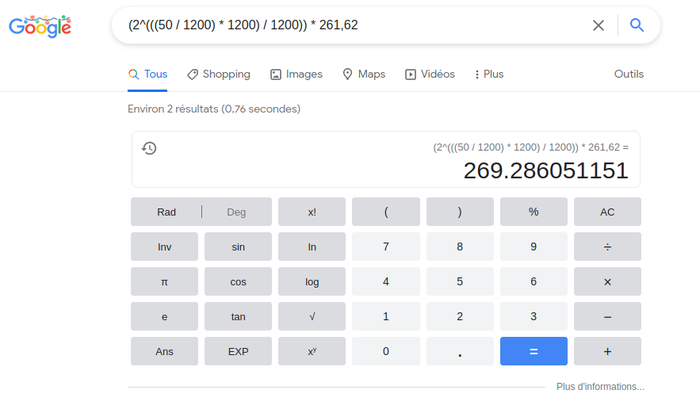
Autres numérateurs : 16,16 (1/12e) d.t [72 sons] – 18,18 (1/11e) d.t [66 sons] – 20 (1/10e) d.t [60 sons]
22,22 (1/9) d.t [54 sons] – 25 (1/8e) d.t [48 sons] – 28,57 (1/7e) d.t [42 sons] – 33,33 (1/6e) d.t [36 sons]
40 (1/5e) d.t [30 sons] – 66,66 1/3e d.t [18 sons] – (100 1/2 ton).
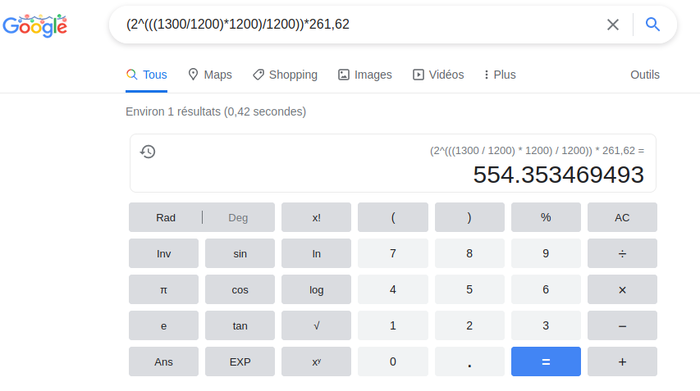
segment (Ep ÷ mod] ∼ (1300/1200)
(2^(((1300/1200)*1200)/1200))*261,62 D5 8ve
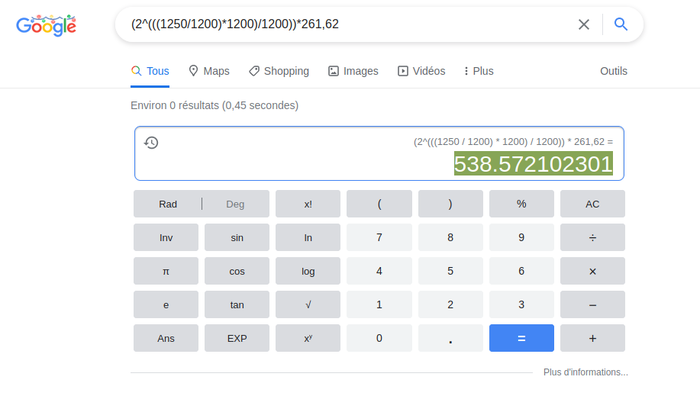
segment (Ep ÷ mod] ∼ (1250/1200)
(2^(((1250/1200)*1200)/1200))*261,62 C5 + 50 cents
Octave proliférante et (X)aves →
Ratio f2 / f1
523,24 / 261,62 = 2(8ve)
(2^(((1200 / 1200) * 1200) / 1200)) * 261,62
———————————————–
Logarithmes & opérations élémentaires →
log(523.24 + 261.62) = 2.89479219604 soit 261.62 * (2.89479219604 ^1) = 757.335534328 Hz [F#5 + 40 cents ∆]
log(523.24 – 261.62) = 2.41767094133 soit 261.62 * (2.41767094133 ^ 1) = 632.511071671 Hz [C#5 + 28 cents∆]
[ Réduction sonopoïétique log(261.62) * 261.62 = 632.511071669 (vérification) ]
log(523.24 * 261.62) = 5.13637187831 soit 261.62 * (5.13637187831 ^ 1) = 1343.7776108 Hz [E6 + 33 cents ∆]
log(523.24 / 261.62) = 0.30102999566 soit 261.62 * (0.30102999566 ^ 1) = 78.7554674646 (constante K cents ou fréquentielle)
X(ave) d’origine (2^(((1250 / 1200) * 1200) / 1200)) * 261,62 = 538.572102301
(dépassement de l’octave)
538.5721022301 / 261.62 = 2.05860447301 C4 + 50 ∆
Logarithmes
Log(538.5721022301+ 261.62) = 2.90319426065 [F#5+45∆] soit 261.62 * (2.90319426065 ^ 1) = 759.533682471 [F#5+45∆]
Log(538.5721022301 – 261.62) = 2.44240466605 [C#5 + 50∆] soit 261.62 * (2.44240466605 ^ 1) = 638.981908732 [D#5 + 46∆]
Log(538.5721022301 * 261.62) = 5.14891479474 [E6 + 37∆] soit 261.62 * (5.14891479474 ^ 1) = 1347.0590886
Log(538.5721022301 / 261.62) = 0.31357291209 soit 261.62 * (0.31357291209^1) = 82.036945261 (constante K cents ou fréquentielle)
X(aves) logarithmiques dérivées à partir des intervalles du modulo 12
Log(100) = 2
Log(100) ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 523.24 8ve
soit : 2 ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 8ve
Log(200) = 2.30102999566
(log200 ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 601.99546746
[1443 cents ou (1) 8ve + 243 cents] Réalité sonore
Log(300) = 2.47712125472
(log(300) ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 648.06446266 Hz
[1570 cents ou (1) 8ve + 370 cents]
Log(400) = 2.60205999133
(log(400) ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 680.750934931 Hz
[1656 cents ou (1) 8ve + 456 cents]
Log(500) = 2.69897000434
(log(500) ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 706.104532534 Hz
[1719 cents ou (1) 8ve + 519 cents
Log(600) = 2.77815125038
(log(600)^(((1200 / 12) * 12) / 1200)) * 261.62 = 726.819930125 Hz
[1769 cents ou (1) 8ve + 519 cents]
Log(700) = 2.84509804001
(log(700) ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 744.334549229 Hz
[1810 cents ou (1) 8ve + 610 cents]
Log(800) = 2.90308998699
(log(800) ^ (((1200 / 12) * 12) / 1200)) * 261.62 =
759.506402397 Hz [1845 cents ou (1) 8ve + 645 cents]
Log(900) = 2.95424250944
(log(900) ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 772.88892532 Hz
[1875 cents ou (1) 8ve + 675 cents]
Log(1000) = 3
(log(1000) ^ (((1200 / 12) * 12) / 1200)) * 261.62 =784.86 Hz
[1902 cents ou (1) 8ve + 702 cents]
Log(1100) = 3.04139268516
(log(1100)^(((1200 / 12) * 12) / 1200)) * 261.62 = 795.689154291
[1926 cents ou (1) 8ve + 726 cents]
Log(1200) = 3.07918124605
(log(1200)^(((1200 / 12) * 12) / 1200)) * 261.62 = 805.575397591
[1947 cents 1) 8ve + 1947 cents]
Épilogue
261.62 * (2 ^ 1) = 523.24
log(523.24 / 261.62) = 0.30102999566
0.30102999566 * 1000 = 301.02999566
Log(2) = 0,30102999566 références
Calculette sonoïètique
Tradition / continuité / dépassement
B(e) ^ (((Ep ÷ mod) × d) ÷ Ea)) × f° = ms
Base initiale concaténée à un espace de parcours divisé par le modulo, multiplié par un déplacement. Le tout divisé par l’espace auxiliaire d’itération et clôturée par la multiplication d’une fréquence.
Opérations élémentaires avec l’8ve
↑ (4^(((1200 / 12) * 12) /1200)) * 261,62 = 1046.48 Hz ( 8^, 16^, 32^, 64^, etc.)
╪ (2^(((1200 / 12) * 12) / 1200)) * 261,62 = 523.24 Hz
↓ (2^(((1200 * 12) * 0) / 1200)) * 261.62 / 2 = 130.81 Hz (÷4, ÷8, ÷16, etc…)
Opérations avec la variable (d) déplacement
(2^(((1200 / 12) * (1) / 1200)) * 261,62 = 277.176734746 [C#4]
(2^(((1200 / 12) * (-1)) / 1200)) * 261,62 = 246.936397684 [B3]
Etc…
Continuité
Quelques partages infra-chromatiques dans l’8ve
∆ : cent(s)
Modulo 72 échelle douzièmes de ton 261.62 * (2^(((1200 / 72) * 1) / 1200)) = 264.150789763 [C41/12 + 17 (∆)]
Modulo 66 échelle onzièmes de ton 261.62 * (2^(((1200 / 66) * 1) / 1200)) = 264.382071985 [C41/11 + 18 (∆)]
Modulo 54 échelle neuvièmes de ton 261.62 * (2^(((1200 / 54) * 1) / 1200)) = 264.999815076 [C41/9 + 22 (∆)]
Modulo 42 échelle septièmes de ton 261.62 * (2^(((1200 / 42) * 1) / 1200)) = 265.973471754 [C41/7 + 29 (∆)]
Modulo 30 échelle cinquièmes de ton 261.62 * (2^(((1200 / 30) * 1) / 1200)) = 267.735077624 [C41/5 + 40 (∆)]
Modulo 24 échelle quarts de ton 261.62 * (2^(((1200 / 24) * 1) / 1200)) = 269.286051151 [C41/4 + 50 (∆)]
Modulo 22 échelle Shrutis 261.62 * (2^(((1200 / 22) * 1) / 1200)) = 269.994006144 [C41/4+4∆ + 54 (∆)]
Modulo 18 échelle tiers de ton 261.62 * (2^(((1200 / 18) * 1) / 1200)) = 271.890998714 [C41/3 + 67 (∆)]
Échelle chromatique 261.62 * (2^(((1200 / 12) * 1) / 1200)) = C41/2
Dépassement : notre vision →
FIN
Théorie musicale I