
II
Aritmética y combinatoria “heurísticas”
Apuntes para un curso imaginario
Hibridación de las cuatro categorías básicas en el fenómeno sonoro frecuencial
Exordio
En el recomienzo irrumpe la más pequeña magnitud concebida en nuestra percepción acústica: 2^(1/1200)equivalente a 1.00057778951 (valor de un cent) ―y que remite a la primera magnitud en el recorrido de una serie (escala logarítmica) de 1200 cents, asociada a la 8va.
Desde entonces, la comunidad científica de la época, autoriza el empleo de este resultado para la comprensión civilizada de nuestras sensaciones auditivas: 2^(100/1200) equivalente a 1.05946309436 e igual a un semitono cromático.
…y todo esto es posible gracias a las investigaciones llevada a cabo por Alexander John Ellis científico, analista y lingüista a saberes múltiples (1814-1890).
¡Eureka!
Con la célebre formulación 2^(100/1200) ―que en realidad se reduce a 2^(1/12)― se consolida la “potencia binaria” como rectora sin contesta de la música occidental y regenta a su vez, la distribución definitiva de los 12 términos (del o de un) ciclo cromático *.
Surge así, la deliciosa categoría oído absoluto (con su estándar de referencia a 440); a nuestro modesto entendimiento, la capacidad de “distinguir” 12 frecuencias en lugar de 1200 y que normativamente ignora las diferencias incluso metodológicas, como por ejemplo: la realidad acústica del cent en un pequeño recorrido de 1 semitono, las nueve comas ¡fundadoras del pensamiento occidental! ♫: incluso, aún en nuestros días, el desconocimiento de la escala (prácticamente clásica) del compositor de origen ruso Ivan Wyschnégradsky (1893-1979) y en fin, los trabajos fundamentales de Julián Carrillo.
Afortunadamente, la historia del tratado no es la historia del pensamiento musical.
De esta manera, con los trabajos de J. A. Ellis, surgen también otras interrogantes y por supuesto otras perspectivas: el estudio de músicas no occidentales e incluso más antiguas que aquella auto-proclamada como universal y en fin, una legitimación del universo infra-cromático —que en nuestro caso, preferimos denominarlo infra-audio-frecuencial.
En ese sentido, los trabajos de J. A. Ellis son también patrimonio de todos los imaginarios sonoros que constituyen la diversidad cultural planetaria.
…Y tal como ya lo hemos señalado en otras ocasiones, la problemática no comienza con J. A. Ellis; la mencionada ya tenia lugar desde hacía casi dos milenios en el imbroglio de las “comas” a través de los siglos: Pitágoras, Zarlino (1517-1590), Mercator (1512-1594), etc; seguido delsistema general de los intervalos y los sonidosde JosephSauveur (1653-1716), las investigaciones acústicas de Félix Savart (1791-1841) e incluso de otros investigadores, para finalizar con la llegada de los cents con J. A. Ellis.
Pasemos entonces a la parte ardua de la problemática y para ello recordemos un corolario ya anunciado en un precedente cuaderno abierto.
Recordemos que la méride de Sauveur equivale a 27,9069767442 (redondeado a 28 cents en un recorrido de 1200: a su vez, la eptaméride (unidad más pequeña aún) equivale a 3,986710963 cents (redondeado a 4 cents).
Por otra parte, si 1 Savart vale 4 cent(s), y una “coma” 5 savarts, tendremos entonces una operación de 4*5 cents sea 20 cent(s) + 2 cents por coma (equivalente aproximadamente a 22,22 cents en un recorrido de 200); sin embargo, recordemos que 1 tono (200 cents) posee 9 comas / (200/9) −con una distribución de 5 comas por la magnitud cromática (200/9)*5 y 4 comas por la magnitud diatónica (200/9)*4.
Dado entonces que las cuatro categorías ya mencionadas acuerdan un compromiso en el recorrido de los 1200 cents, deducimos que 300 pasos en lo concerniente al sauveur y el savart, adicionados a 9 comas y distribuidos en 6 segmentos de 50 términos constituyen la totalidad de los componentes del espacio a operar.
En cuanto a la comas, éstas tendrán lugar cada 22 cents (como eventos configuracionales potencializados).
Procedimientos heurísticos para el calculo de nuestra proposición
261,63*1,00057778950655 ^ 4 = 262.235192533 Hz
261,63 Hz*1,00057778950655 ^ 20= 264.669994166 Hz
1200 * log (264.975929614 Hz /261.63 Hz) / log (2) = 21.9999999969 cents (redondeado a 22 )
sea 261,63*(2^ (5,5/300)) =264.975929614 (magnitud del primer COMA)
f *2^(m / t)
Submódulo (1200/4)/6
Primer segmento: Hibridación
Observación I
Primera extensión heurística
Efectivamente, el despliegue frecuencial que se obtiene con el recorrido de 200 cents al igual que el mismo obtenido en 200*6, revela claramente la presencia de un evento potencializado constituido por el ciclo de magnitudes de las comas ―con el objeto de enactar entre el semitono cromático/semitono diatónico o viceversa una pasarela: 4+5 o 5+4 comas.
Ahora bien, todo pareciera indicar que en la idea de la noción de 8va y el constructo epistémico *que legitima su existencia, a saber el temperamento, estuvo y está aún presente en el tratado, mas no en la historia del pensamiento musical, el quiebre de una simetría de la alteridad —y posiblemente, la búsqueda sin contesta de una identidad sonora de índole universal.
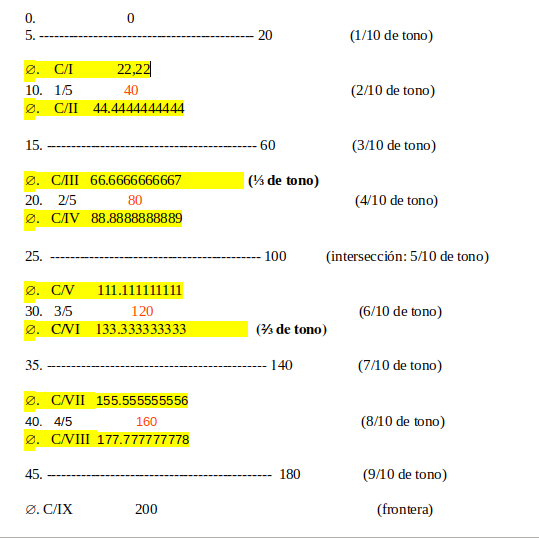
El cuadro precedente extraído de los 50 pasos del primer segmento señalan la proliferación espacial de las 7 magnitudes constitutivas del eje ausente en estado de potencialización. Se trata en definitiva, de la sucesión de tercios y quintos de 200 cents ―conocidos tradicionalmente como los tercios y quintos de tono.
He aquí primeramente el ciclo de quintos de tono aparecidos en la actualización:
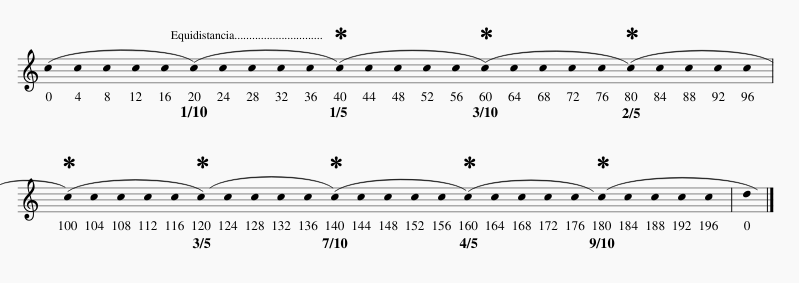
 Quintos extraídos
Quintos extraídos
Seguidamente el ciclo de COMAS con tercios de tono:

El Metamorfoseador de Julián Carrillo
Darmstadt Aural Documents, Box 4: Pianists
Luego de toda esta especulación heurística, emerge una cierta duda acerca de la limitación o no de ese territorio definido históricamente como la 8va.
En efecto, entendemos que el territorio evocado no es fundamentalmente una exclusividad del conjunto cromático. De hecho, a todo lo largo del siglo XX, diversos creadores se habían interrogado a menudo sobre esta problemática: Julián Carrillo, Ivan Wyschnegradsky, Alois Haba, Claude Ballif (entre otros); éste último ―padre de la METATONALIDAD― y heredero directo de las investigaciones de Wyschnegradsky, nos enseña que las estrategias compositivas surgen como sistemas dinámicos, flexibles y abiertos ―para acoger en sus cimientos una aproximación cuasi sistémica del proceso sonoro.
Este enfoque, otorga un valor fundamental a la interacción de los efectos frecuenciales (tanto en el recorrido sonoro como en la percepción global de los mismos) y proyecta así, los modelos referenciales elásticos ―utilizables en cualquier momento como mecanismos de acción o decisión.
Henos aquí frente a un sistema sin ánimo de sistemaque integra la “duratividad “ a distancia entre microforma y macroforma.
Por último, una intuición nos aborda repentinamente : ¿será que la noción de octava, mas no su concepto, se trastoca con alguna forma de entendimiento? Nos parece que semejante respuesta, correspondería al campo histórico de las ideas.
De nuestro lado, continuemos con el concepto (claro está si la octava lo posee) y digamos entonces, parafraseando a Werner Karl Heisenberg, cuando nos señala en su Manuscrito de 1942 (a propósito del lenguaje) que la importancia de los conceptos no residen en su precisión sino sobre todo en su fecundidad. Por su parte, Stephane Lupasco nos señala que el concepto consiste en un conflicto de devenires lógicos engendrados por el dinamismo de una dualidad antagonista —imprescindible para la aprehensión de su estructura); así, tomar consciencia del concepto, significa pasar alternadamente de su comprensión a su extensión y viceversa (fuente).
____________________________________________________________________________
Observación II
La Equis(ava) / Dos divertimenti
Primer divertimento
Puesto que hemos evocado el reemplazamiento de la 8va por otro territorio, nuestra gestión heurística tendrá el deber de considerar históricamente, el proceso de reflexión que condujo a la reemplazada a determinar su legitimidad:
Alexander John Ellis 1885
2^(1/1200) 1.00057778951 (centésima de semitono temperado)
2^(1/100) 1.00695555006 (semitono temperado)
Heurística lúdica I
Primer divertimento de caso (operación con algunos términos de la serie Fibonacci).
Nuestro ejercicio consistirá en modificar la base que origina la equidistancia esotérica que constituía el Diabolusinmusica para el oído refinado durante el medioevo.
Procederemos entonces en tanto que profanos y escogeremos así, una base inesperada: el numero áureo.
1,618 (número áureo) [*]
Comencemos antes que nada por detectar la existencia de un primer paso logarítmico:
1.618^(1/1.618) = 1.0045771591
Procedamos a anexar nuestra frecuencia substrato multiplicada por la nueva formulación
261,63*1.618^(1/1.618) = 262.827522134
verifiquemos su recorrido en cents
(1200 × log(262.827522134 ÷ 261.63) ÷ log(2) = 7.90605381145 cents redondeado a (8)
f1 261.63 Hz – f2 262.827522134 Hz =
Utilicemos la misma cantidad de términos del espacio que deseamos reemplazar
261,63*1.618^(12/1.618) = 276.367604811
verifiquemos una vez su recorrido en cents
(1200 × log( 276.367604811÷ 261.63) ÷ log(2) = 94.872645768 cents redondeado a (95)
Procedamos a la resta 100-95 = 5 cents: el resultado corresponde al quinto término de la serie Fibonacci.

Adicionemos un término a la siguiente formulación:
261,63*1.618^(12/1.618)+1 = 277.367604811
Verifiquemos una vez más su recorrido en cents
(1200 × log( 276.367604811÷ 261.63) ÷ log(2) = 101.125583638 cents redondeado a (101)
Decisión : nuestra escala poseerá 12 términos y sus componentes obedecerán a los 12 primeros términos de la serie Fibonacci (1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144). Bien entendido la cifra “0” corresponde a la nota substrato.
He aquí su despliegue: la cifra 1 en nuestra formulación corresponde al primer término de la serie Fibonacci.
261,63*1.618^(0/1.618) (1200 × log( 261.63÷ 261.63) ÷ log(2) 0 cents
261,63*1.618^(1/1.618)(1200 × log( 262.827522134÷ 261.63) ÷ log(2) 8 cents
261,63*1.618^(2/1.618)(1200 × log( 262.827522134÷ 261.63) ÷ log(2) 16 cents
261,63*1.618^(3/1.618) (1200 × log( 265.23903524÷ 261.63) ÷ log(2) 24 cents
261,63*1.618^(5/1.618) (1200 × log( 267.672674625÷ 261.63) ÷ log(2) 40 cents
261,63*1.618^(8/1.618)(1200 × log( 271.365065083÷ 261.63) ÷ log(2) 63 cents
261,63*1.618^(13/1.618) (1200 × log( 277.632583307÷ 261.63) ÷ log(2) 103 cents
261,63*1.618^(21/1.618) (1200 × log( 287.963093064÷ 261.63) ÷ log(2) 166 cents
261,63*1.618^(34/1.618) (1200 × log( 305.576338434÷ 261.63) ÷ log(2) 269 cents
261,63*1.618^(55/1.618) (1200 × log( 336.332636099÷ 261.63) ÷ log(2) 435 cents
261,63*1.618^(89/1.618) (1200 × log( 392.826875491÷ 261.63) ÷ log(2) 703 cents
261,63*1.618^(144/1.618) (1200 × log( 504.989865705÷ 261.63) ÷ log(2) 1138 cents

Recursividad frecuencial
El término 144 de la serie Fibonacci equivale al término 12 multiplicado por 12, sea
261,63*1.618^(1/555565404224292694404015791808)= 261.63
Las tres leyes de la recursividad
Los primeros pasos de la serie Fibonacci
Clausura del primer divertimento…
Segundo divertimento
Heurística lúdica II
Un espacio referencial *
(1.618^(1/1.618))*261.63 = 352.246008795
f1 261.63 Hz – f2 352.246008795 Hz =
(1.618^(0.1/1.618))*261.63 = 269.527693728
f1 261.63 Hz – f2 269.527693728 Hz =
Sea
(1.618^(0.2/1.618))*261.63 / 102.9732916326906 cents
(1.618^(0.3/1.618))*261.63 / 154.4599374507201 cents
(1.618^(0.4/1.618))*261.63 / 205.9465832714247 cents
(1.618^(0.5/1.618))*261.63 / 257.4332290877854 cents
(1.618^(0.6/1.618))*261.63 / 308.91987490072 cents
(1.618^(0.7/1.618))*261.63 / 360.406520720242 cents
(1.618^(0.8/1.618))*261.63 / 411.89316653979137 cents
(1.618^(0.9/1.618))*261.63 / 463.3798123533017 cents
(1.618^(1.0/1.618))*261.63 / 514.8664581696748 cents = (1.618^(1/1.618))*261.63
Clausura modular
Espacio referencial: F + 15 cents o 515 cents (extremo máximo)
Recorrido: 515 /10 = 51.5 (constante de la escala operada, asociada a los cents)1.03018649898
1.03018649898*261.63 = 269.527693728

Una paradoja acústica residual
515*1 = 515 F/15c – 515*2 = 1030 Bb/30c – 521*3 = 1545 Eb/45c – 521*4 = 2060 Ab/60c – 521*5 = 2575 Db/75c – 521*6 = 3090 Gb/90c – 515*7 = 3605 C/05c – 515*8 = 4120 F/20c – 515*9 = 4635 Bb/35c – 515*10 = 5150 Eb/50c – 515*11 = 5665 Ab/65c – 515*12 = 6180 Db/80c – 515*13 = 6695 Gb/95c – 515*14 = 7210 C/10c.

En fin, para los amantes de la sagrada octava, su aparición no se hará esperar:
1.03018649898*261.63*2 = 539.055387456 / 1251.4866458184042 cents.
Sea (1200 + 51.4866458184042) o si el lector prefiere 1252cents.
f1 261.63 Hz – f2 539.055387456 Hz =
Henos aquí, frente a una octava dilatada: terminología perteneciente a Ivan Wyschnegradsky y desarrollada en sus investigaciones expuestas en La loi de la pansonorité.
En cuanto a los doce términos semejantes a los de la escala cromática, cada grado tendrá sistemáticamente 1252/12, sea una constante de 104.333333333 cents.
Sin embargo, para aquellos que deseen un retorno a la 8va justa asociada a la serie Fibonacci, el paso 152, puede eventualmente satisfacer el deseo. En ese caso, se puede obtener una escala de 152 términos que un recorrido de 1200 cents equivale a una constante de 7.89473684211 cents que se puede redondear a 8.
(1.618^(152/26099748102093884802012313146549))*261,63 = 261.63
(1.618^(1/26099748102093884802012313146549))*261,63 = 261.63
(1.618^(0/26099748102093884802012313146549)) = 1
(1.618^(1/26099748102093884802012313146549)) = 1
Por el contrario, en el caso especifico de nuestro procedimiento: la “equisava” asociada al número áureo 1.618, sería equivalente a 1.618/152 y su constante a 10.6447368421 cents ―que arbitrariamente no habremos de redondear.
————————————————————————————————————————-
Memento
Procedimientos de verificación para el cálculo de los cents
Con la calculadora Google
(1200 × log(261.63 ÷ 440)) ÷ log(2) = -899.970654865 (redondeado a menos 900)
(1200*log(C4 / A4)) / log(2) = – 900 cents
(1200 × log(440 ÷ 261.63)) ÷ log(2) = 899.970654865 (redondeado a más 880)
(1200*log(A4 / C4)) / log(2) = + 900 cents
Con las herramientas HyperPhysics
Procedimientos para el calculo de algunas escalas micro-tonales octavantes*
1200/24 (escala de 24 sonidos con constante de 50 cents equivalente a ¼ de tono)
Realidad frecuencial: 440*2^(1/24) = 452.892984123
Realidad material / Inspector de MuseScore

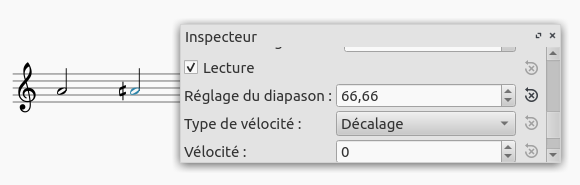
1200/18 (escala de 18 sonidos con constante de 66,66 cents equivalente a 1/3 de tono)
Realidad frecuencial: 440*2^(1/18) = 457.274059454
Realidad material / Inspector de MuseScore
1200/30 (escala de 30 sonidos con constante de 40 cents equivalente a 1/5 de tono)
Realidad frecuencial: 440*2^(1/30) = 450.284512479
Realidad material / Inspector de MuseScore

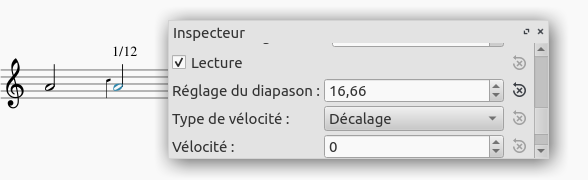
1200/72 (escala de 72 sonidos con constante de 16,66 cents equivalente a 1/12avo de tono)
Realidad frecuencial: 440*2^(1/72) = 444.256354621
Realidad material / Inspector de MuseScore
_______________________________________________________________
Realidad frecuencial: 440*2^(1/22) = 454.083643083

1200/22= 54.5454545455 cents / sea: 54.5454545455*(2,3,4 ………..22)
Frecuencias: 440*2^(54,5454545455*1/1200) multiplicación por (1,2,3 …………. 22)
(((1200 log(880 ÷ 440)) ÷ log(2) ÷ (12 + 10) × 1))= 54.5454545455 (constante cents)
(((1200 log(880 ÷ 440)) ÷ log(2) ÷ (12 + 10) × 22)) = 1200 (espacio de acogida)
Música clásica de la India y occidental: Algunas comparaciones
___________________________________________________________________
Peroratio
No podemos finalizar este segundo cuaderno, sin precisar al amable lector que el resultado de nuestros cálculos, tienen lugar luego de una formulación específica.
Dicho de otra manera, ellos responden a una estrategia singular en el recorrido de un espacio sonoro imaginado a niveles de realidad múltiples / lectura.
Por consiguiente y afortunadamente para el hacer sonopoiético las implementaciones son infinitas.
La finitud la fija el usuario…
P. S.: Deseamos precisar a nuestros amables lectores que la herramienta para una eventual escucha y por supuesto la confección de partituras, el editor MuseScore cumple con los requisitos necesarios. Él es además, completamente gratuito y eficaz para todo tipo de plataforma. En cuanto a los cálculos ―y aún dentro del espíritu delsoftware libre al cuaderno de notas inventivo―, la calculadora de Google, así que el entorno de exploración HyperPhysics deberían bastar.
No obstante, si la extensión de los procedimientos lo exige, la hoja de cálculo de Libre Office, podría ser de buena ayuda y completar además un pequeño taller virtual.
