…Y puesto que el centum (cent ∆) consiste en una magnitud logarítmica que define la distancia entre dos frecuencias (f2) y (f1) en un temperamento igualitario:
ej. 523.24 Hz / 261.62 Hz = 2 ≡ log(100) = 2
Aplicaremos entonces el mismo principio a la construcción de otras magnitudes diferentes a la tradicional octava 8va.
Por ejemplo
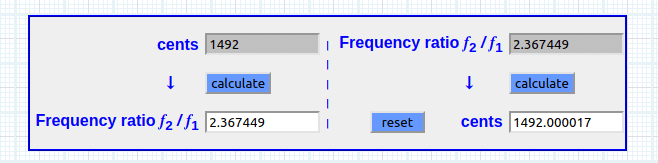
Sea una equisava de 1492 pasos que escogeremos como la frontera de un recorrido frecuencial semejante al valor máximo de 1200 cents por 8va ─con su valor mínimo substrato de 100 cents para el semitono:
((1492 * log((523.24 / 261.62))) / log(2) / (1492 / 100) = 100
Obtenemos así, un nuevo circuito de (1492÷12) términos con un valor mínimo dilatado de 124.33 ∆
y su retorno al valor mínimo substrato con la operación (1492÷100) = 14.92 términos
Empero, toda transformación supone la presencia de algo que se va a transformar:
(2^ (((1492 / 12) * 12) / 1200)) * 261,62 = 619.37200141
Veamos:
(yuxtaposición) 2 ^ (1492 / 1200) = 2.36744897718 Ratio (cents)
2 ^ (1492 / 1200) * 261.62 Hz = 619.37200141 Hz o log(100) ^ (1492 / 1200) * 261.62 Hz = ídem
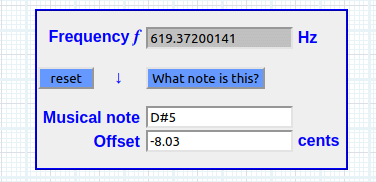
Verificación: equisava 1492 ∆
BIFURCACIÓN / PROLIFERACIÓN
2.36744897718 ^ (1492 / 1200) * 261.62 = 763.88243193 Hz
763.88243193/ 261.62 = 2.91981664984
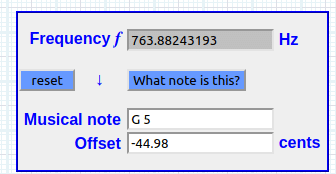
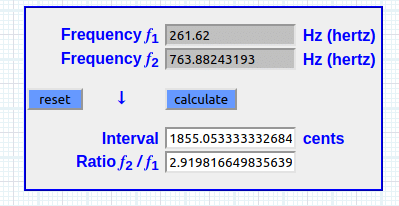
sea un recorrido de una 8va + 655 cents
Equisava de fuerza resultante a partir de la fuerza neta de una frecuencia logarítmica
log(261.62) * 261.62 = 632.511071669 Hz
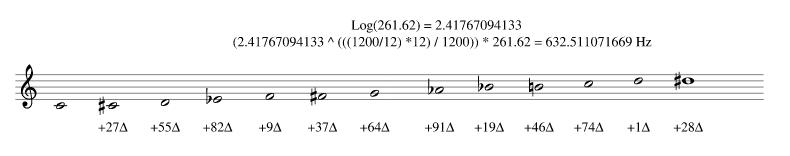
Verificación
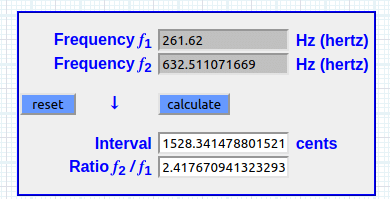
Despliegue de una frecuencia logarítmica (sonido substrato)
(log261.62^(((1200/12)*0)/1200))*261.62 = 0 [C4] + 0 Hz

(log261,62^(((1200/12)*1)/1200))*261,62 = 52.7092559725 Hz [G#(1 ) + 26]
(log261,62^(((1200/12)*2)/1200))*261,63 = 105.418511945 Hz [G#(2) + 26]
(log261,62^(((1200/12)*3)/1200))*261,62 = 158.127767917 Hz [D#(3) + 28]
(log261,62^(((1200/12)*4)/1200))*261,62 = 210.83702389 Hz [G#(3) + 26]
(log261,62^(((1200/12)*5)/1200))*261,62 = 263.546279862 Hz [C(4) + 13]
(log261,62^(((1200/12)*6)/1200))*261,62 = 316.255535835 Hz [D#(4) + 28]
(log261,62^(((1200/12)*7)/1200))*261,62 = 368.964791807 Hz [F(4) + 95]
(log261,62^(((1200/12)*8)/1200))*261,62 = 421.67404778 Hz [G#(4) + 26]
(log261,62^(((1200/12)*9)/1200))*261,62 = 474.383303752 Hz [Bb(4 )+ 30]
(log261,62^(((1200/12)*10)/1200))*261,62 = 527.092559725 Hz [C(5) +13]
(log261,62^(((1200/12)*11)/1200))*261,62 = 579.801815697 Hz [C#(5) + 78]
(log261.62^(((1200/12)*12)/1200))*261.62 = 632.511071669 Hz [D#(5) + 28]
Retorno a la 8va temperada
((1492 * log((523.24 / 261.62))) / log(2) / (1492/100) * 12 = 1200
1492 / 100 = 14.92 (términos)
((14.92/ 12) * 1200) / 14.92 = 100 ∆
