Dialógica maquínica sonoiética
A propósito de nuestra fórmula ⇒
log(100) ^ (((1200/1200) * ((1200/12) * 9)) / 1200) = 1.68179283051 PIL [paradoja: Δ o Hz] ⊕⇒
1.68179283051 * 261.62 = 439.990640317 Hz [A4]
sea: (log(100) ^ (((1200/1200) * ((1200/12) * 9)) / 1200) * 261.62 Hz C4 = 439.990640317 Hz
&
TEMPERAMENTO Joseph SAUVEUR
1 ⇒ 2 ⇒ 4 ⇒ 8 ⇒ 16 ⇒ 32 ⇒ 64 ⇒ 128 ⇒ (256) ⇒ 512 ⇒ 1024 ⇒ 2048 ⇒ (4096) ⇒ 8192 ⇒ 16384… Ver
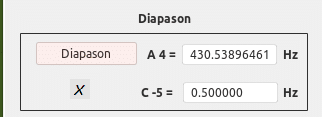
1.68179283051 * 256 = 430.53896461 Hz [A4 Sauveur]
sea: (log(100) ^ ((((1200) / 1200) * ((1200 / 12) × 9)) / 1200) * 256 Hz [C4 Sauveur ↵] = [A4 Sauveur]
o simplemente [ 2 ^ (225 / 300) * 256 = 430.53896461 ]
DIALÓGICA ARITMÉTICA
(log(100) ^ ((((1200) / 1200) * ((1200 / 12) × 12)) / 1200) * 256 = 512 Hz C5
&
Log(512 (C5) Hz / 256 (C4) Hz) = 0.30102999566 [constante (K) Sauveur]
Pero también (diapasón 440) →log(523.24 / 261.62) = 0.30102999566 [constante (K) Sauveur]
Teorema : el recorrido logarítmico espacial de una frecuencia (n) a su 8va equivale a 0.30102999566
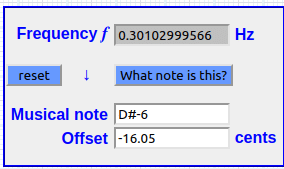
&
Log(2) = 0.30102999566 PIL
Dialógica sonoiética (ej.)
1 ⇒ 2 ⇒ 4 ⇒ 8 ⇒ 16 ⇒ 32 ⇒ 64 ⇒ 128 ⇒ 256 ⇒ 512 ⇒ 1024 ⇒ 2048 ⇒ 4096 ⇒ [8192 ⇒ 16384]
Log(16384 ÷ 8192) = 0.30102999566
0.30102999566 * 256 = 77.063678889 Hz
ESCALADOR
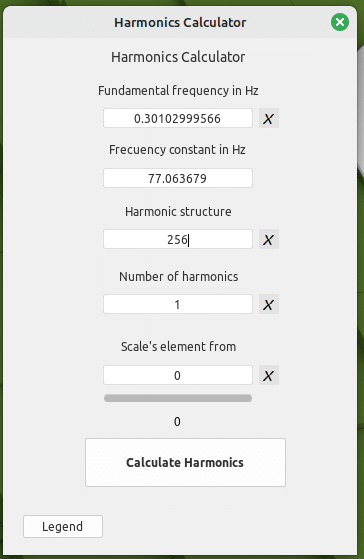

&
Escala PIL Sauveur (o escala de intervalos)
***
Log(100) ^ ((((1200) / 1200) * ((1200 / 12) × 108)) / 1200) * 8 Hz = 4096 Hz
sea 108 pasos: C-1 ⇒ C8
Parámetros Escalador/Sauveur
LIMIT: 512 (256 * 2) / ELEMENTS: 108 [tesitura 9 octavas (escala cromática)]
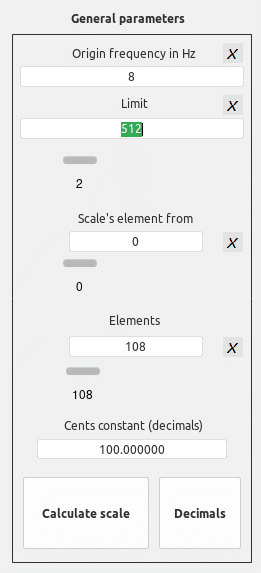
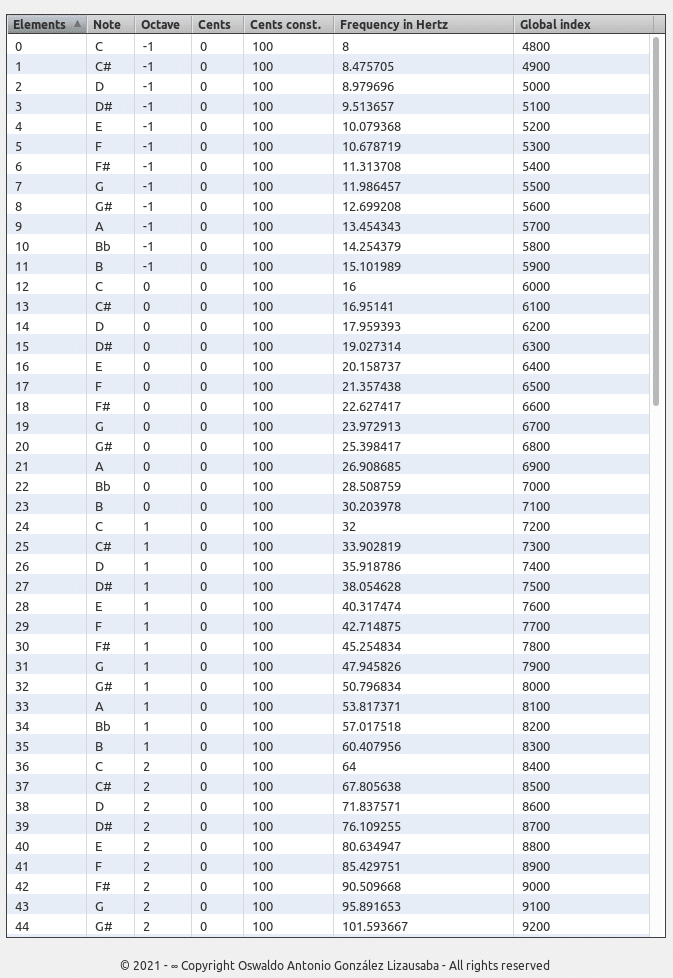
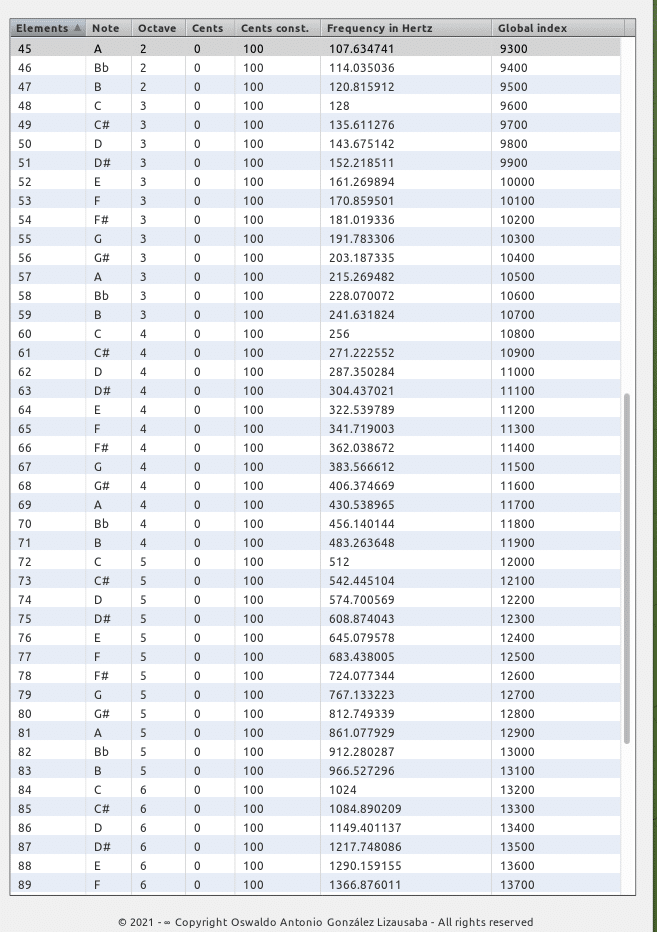
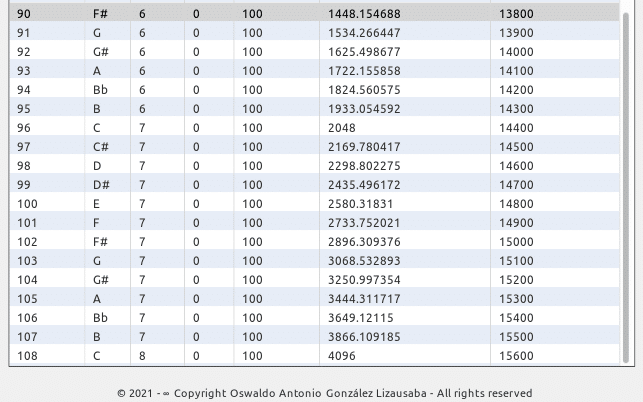
Constante operacional
108 ÷ 2 = 54 tonos enteros [200 cents ∆ = 1T]
sea:
54 * 3 tercios de tono (18) ~ 162 1/3 ⇒ 4096 Hz
54 * 4 cuartos de tono (24) ~ 216 1/4 ⇒ ídem
54 * 5 quintos de tono (30) ~ 270 1/5 ⇒ ídem
54 * 6 sextos de tono (36) ~ 324 1/6 ⇒ ídem
54 * 7 séptimos de tono (42) ~ 378 1/7 ⇒ ídem
54 * 8 octavos de tono (48) ~ 432 1/8 ⇒ ídem
54 * 9 novenos de tono (54) ~ 486 1/9 ⇒ ídem
54 * 10 décimos de tono (60) ~ 540 1/10 ⇒ ídem
54 * 11 onceavos de tono (66) ~ 594 1/11 ⇒ ídem
54 * 12 doceavos de tono (72) ~ 648 1/12 ⇒ ídem
Producto índice logarítmico [PIL⇒]
log(100) ^(((1200 / 1200) * ((1200 / 1200) * 200 / 3)) / 1200) = 1.03925922603 PIL 1/3 de Tono
* 200 / 4)) / 1200) = 1.02930223664 PIL 1/4 ídem
* 200 / 5)) / 1200) = 1.023373892 PIL 1/5 ídem
* 200 / 6)) / 1200) = 1.0194406437 PIL 1/6 ídem
* 200 / 7)) / 1200) = 1.01664043939 PIL 1/7 ídem
* 200 / 8)) / 1200) = 1.01454533494 PIL 1/8 ídem
* 200 / 9)) / 1200) = 1.01291879472 PIL 1/9 ídem
* 200 / 10)) / 1200) = 1.0116194403 PIL 1/10 ídem
* 200 / 11)) / 1200) = 1.01055757199 PIL 1/11 ídem
* 200 / 12)) / 1200) = 1.00967353323 PIL 1/12 ídem
Ejemplo doceavos de tono en un recorrido de 9 octavas…
Escala de Ivan Wyschnegradsky 1893-1979
log(100) ^(((1200 / 1200) * ((1200 / 1200) * 200 / 12 * 72 * 9)) / 1200) * 8 = 4096 Hz
Realización en Escalador
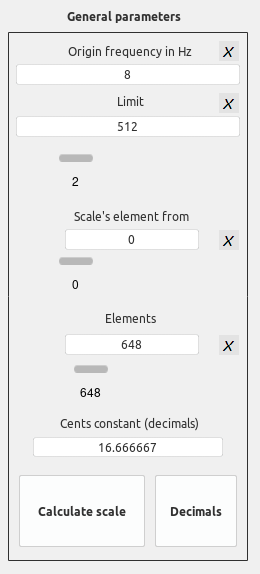

(log(100) ^ (((1200 / 1200) * ((1200 / 72) * 1)) / 1200) = 1.00967353323 [PIL]
1.00967353323 * 8 = 8.07738826584 Hz [C -1 + 17Δ]
sea: (log(100) ^ (((1200/1200) * ((1200/72) * 1)) / 1200) * 8 = 8.07738826583 Hz
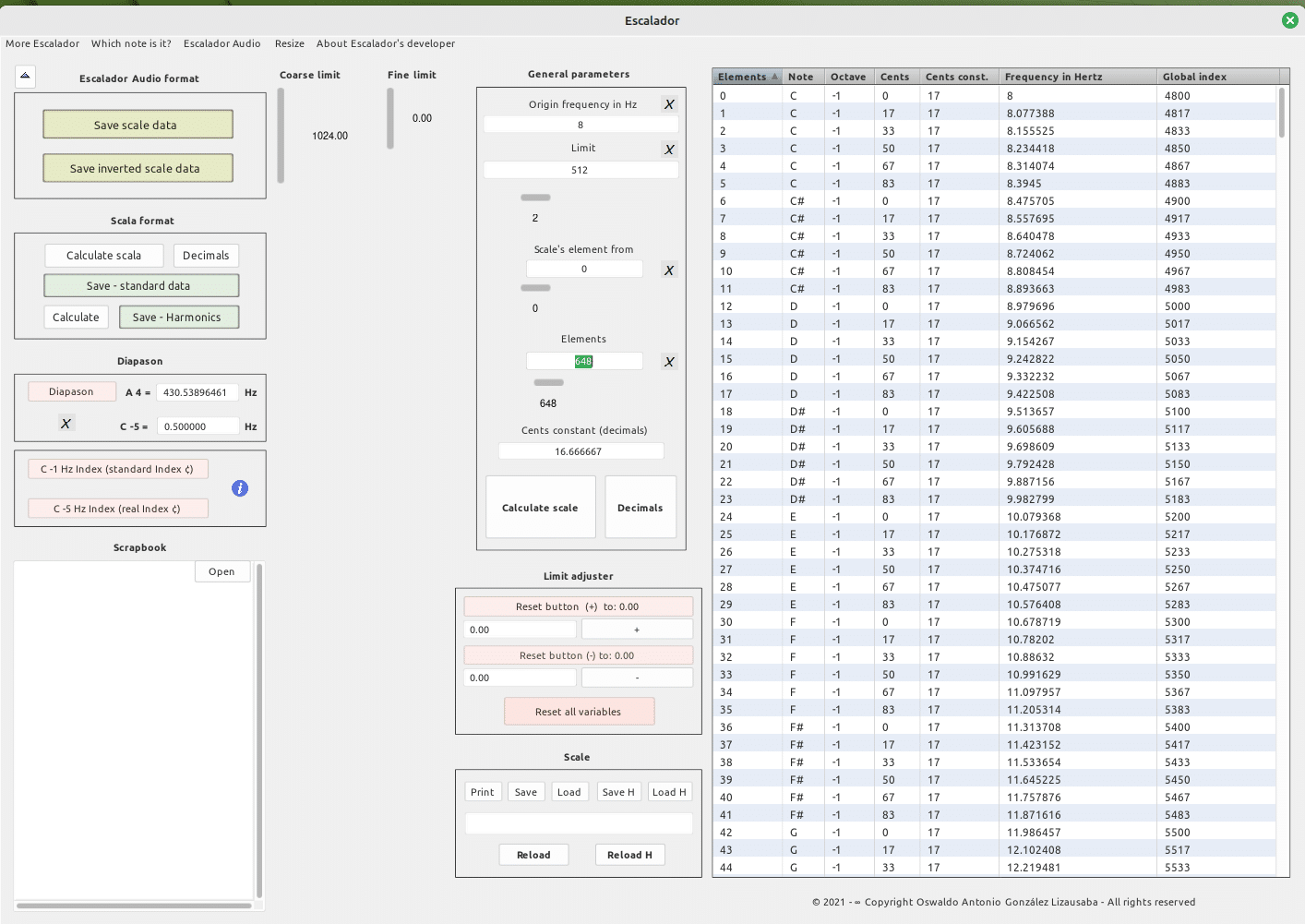
Y así hasta completar 648 pasos…
1 ⇒ 2 ⇒ 4 ⇒ 8 ⇒ 16 ⇒ 32 ⇒ 64 ⇒ 128 ⇒ 256 ⇒ 512 ⇒ 1024 ⇒ 2048 ⇒ 4096 ⇒ 8192 ⇒ 16384
ORIGIN FREQUENCY 8
LIMIT (log(100) ^ (((1200/1200) * ((1200/72) * 648)) / 1200) = 512
RECORRIDO ESPACIAL (log(100) ^ (((1200/1200) * ((1200/72) * 648)) / 1200) * 8 = 4096
En fin, no olvidemos jamás que por ser absolutos los cálculos aritméticos obtenidos en nuestra dialógica sonoiética necesitarán siempre de un vertimiento semántico o significación deseada: sin esta preliminar, no habrá jamás existencia de singularidad alguna…
Ejemplo : ecuación Wyschnegradsky ⇒/Sauveur ⇒
(log(100) ^ ((((300 ÷ 6) ÷ 12) * 864 ÷ 300)) * 8
1 ⇒ 2 ⇒ 4 ⇒ 8 ⇒ 16 ⇒ 32 ⇒ 64 ⇒ 128 ⇒ 256 ⇒ 512 ⇒ 1024 ⇒ 2048 ⇒ 4096 ⇒ 8192 ⇒ 16384 ⇒ 32768
864 pasos
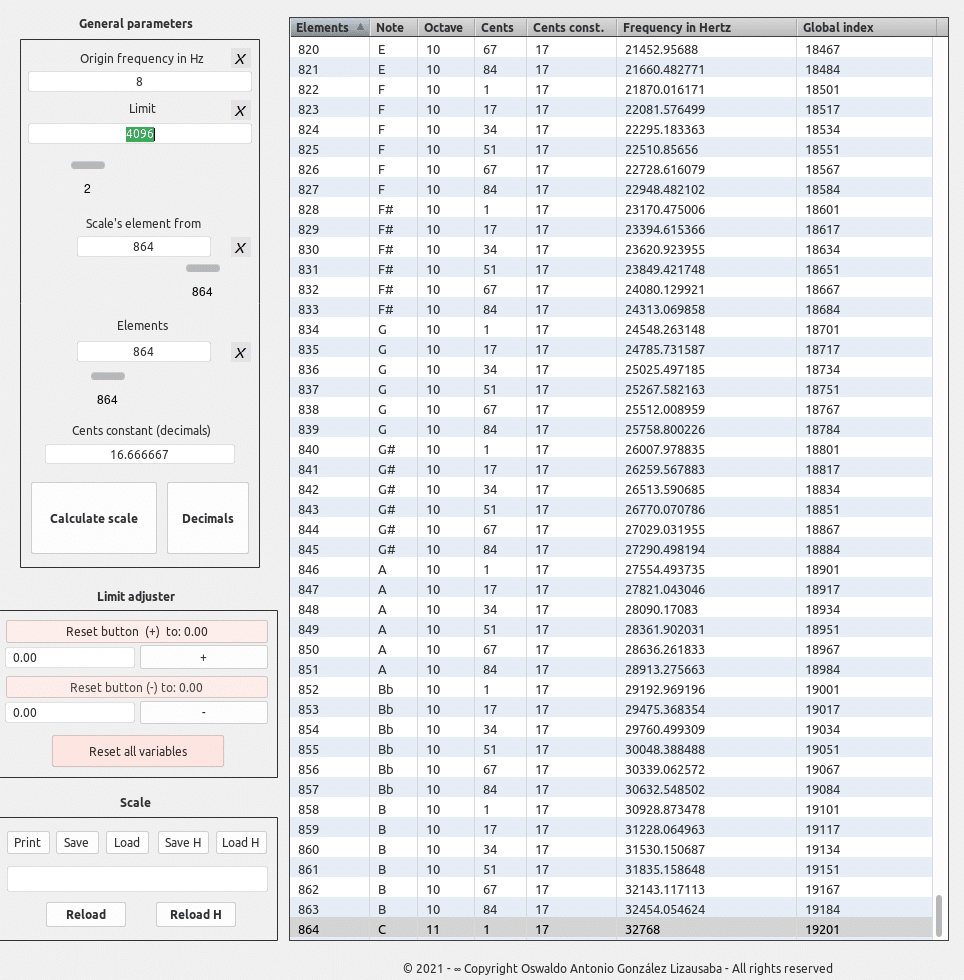
Origen de la especulación
8 Hz ^ (300 / 300) * 4096 Hz = 32768 Hz
1 ⇒ 2 ⇒ 4 ⇒ 8 ⇒ 16 ⇒ 32 ⇒ 64 ⇒ 128 ⇒ 256 ⇒ 512 ⇒ 1024 ⇒ 2048 ⇒ 4096 ⇒ 8192 ⇒ 16384 ⇒ 32768
&
NUESTRA DIALÓGICA
8vas de Sauveur
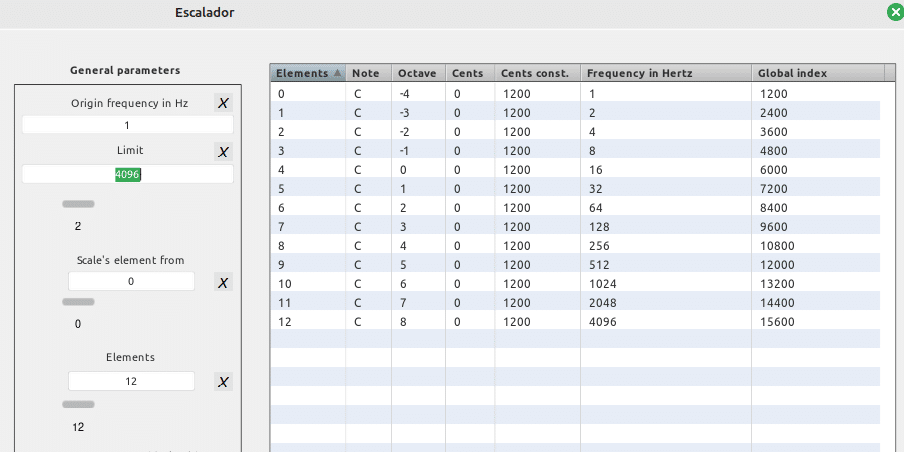
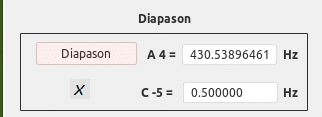
&
Recorrido espacial de las MÉRIDAS de Sauveur
4096 ^ (1 ÷ 512) × 8 = 8.13102651929 | sea: una constante mérida (Km) de 28 cents (Δ)
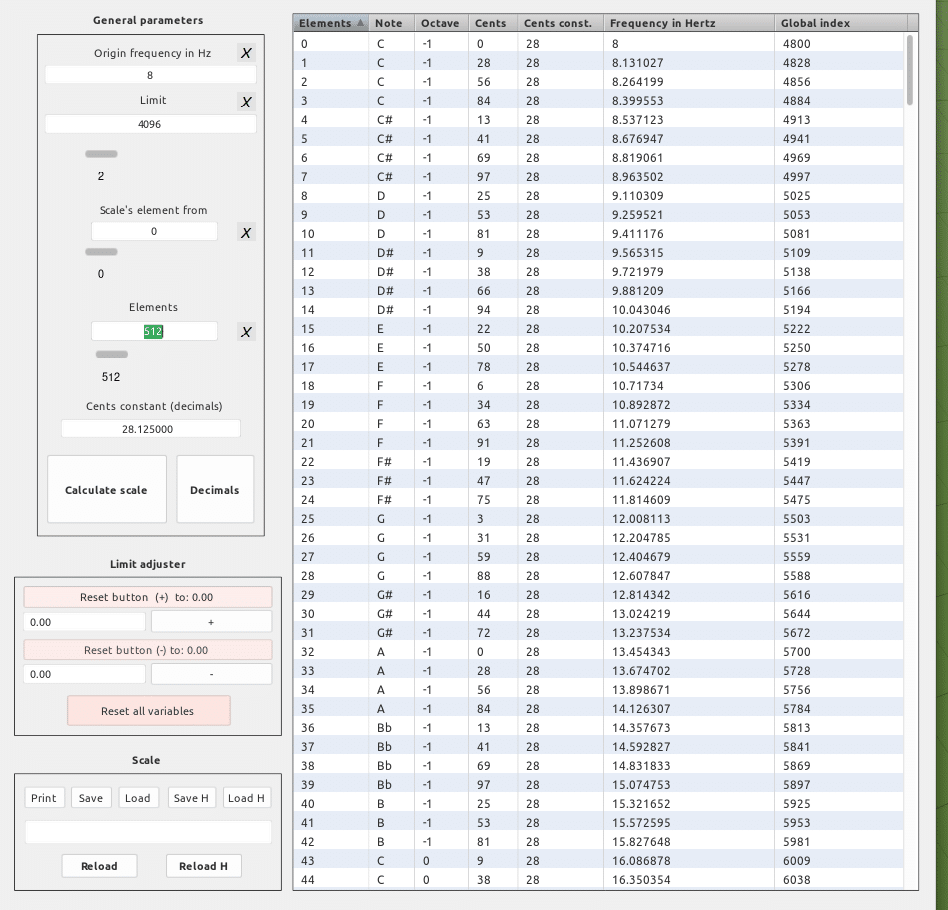
Y así hasta completar 512 pasos
Tesitura global
4096 ^ (512 ÷ 512) × 8 = 32768

Appréhender la chose
&
Y para finalizar, una fórmula Sauveur para todo tipo de cálculo [Ver*] :
Heptaméridas / Méridas / Hercios / Cents / Octavas / Equisavas* /
Diapasones /Espacios Logarítmicos, etc…
(log(100) ^ (((50 ÷ 2) * 9) ÷ 300)) * 256 = 430.53896461 Hz
////////////////////
8va (log(100) ^ (((300 ÷ 12) * 12) ÷ 300)) * 256 = 512 Hz
Pero también ¿ (log(100) ^ (((300 ÷ 12) * 48) ÷ 300)) * 256 ?= →
(log(256) ^ (((300 ÷ 12) * 48) ÷ 300)) * 256 = 8610.71078879 Hz
////////////////////
Escala de Hercios/Méridas -Joseph Sauveur-
PIL⇆ Hz
2 ^ (((300 / 300) * ((300 / 300) * 1Hz)) / 300) = 1.00231316184 PIL⇆ Hz [C -4 ]
2 ^ (((300 / 300) * ((300 / 300) * 300)) / 300)= 2 PIL⇆ Hz [C -3 ]
2 ^ (((300 / 300) * ((300 / 300) * 1)) / 300) * 256 = 256.592169432 PIL⇆ Hz [C4 | 4Δ ∼ 1 heptamérida]
2 ^ (((300 / 300) * ((300 / 300) * 300)) / 300) * 256 = 512 PIL⇆ Hz [C5]
Sea : 300 Hz por 8va (1200 cents/4 heptaméridas)
////////////////////
////////////////////
Un retorno a la norma sera siempre posible de la manera siguiente:
(log(100) ^ (((50 ÷ 2) * 9) ÷ 300)) * 261.62 = A 440
ó
(2 ^ (((300 / 300) * ((((300 / 300) * 300) / 12) * 9)) / 300)) * 261.62 = 439.990640317
