En su Système général des Intervalles des Sons, Joseph Sauveur hace una proposición inusitada con la intención de darle un sentido científico a ese territorio cuasi mítico constituido por la octava.
En efecto, modeliza la distribución del espacio octavante cuando lo divide en 43 partes y cada parte a su vez, en 7 magnitudes aún más pequeñas ─lo que se traduce en 7 * 43 = 301 pasos para “la octava”, redondeados a 300 “sauveurs” o heptaméridas:
(log(100) ^ (((1 / 300) * 300) / 300)) * 261.62 = 262.225169401→ C4 + 4 cents ∼ 1 Hz
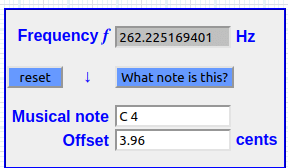
Verificación:
(log(100) ^ (((300 / 300) * 300) / 300)) * 261.62 = 8va
El fundamento de este postulado tiene sus orígenes en el logaritmo decimal de 2.
Log(2) = 0.30102999566 PIL
Corolario
2^(7 ÷ 301) = 1.01625032519 PIL
1.01625032519 × 261.62 = 265.871410076 [1 méride ~ 28 ∆]
28 m ÷ 7 h = 4 × 7 ∆
4 ∆ = 1 Hz
1 méride de saveur = 28 ∆ ÷ 7 heptamérides de sauveur = 4 ∆ ~ 1 sauveur = 1 hertz
(0,301 / 7) = (0,043 * 1000) = 43
Así, una méride equivale a 27,9069767442 centésimas (redondeado tradicionalmente a 28), en un recorrido de 1200 cents, mientras que una eptaméride equivalente a 3,986710963 cents (redondeado tradicionalmente a 4 cents).
Deconstrucción
27,9069767442 × 43 = 1200 ∆
2^(4 / 1200) x 261.62 = 262.225169401
2^((4 × 300) / 1200)) x 261.62 = 523.24
2^(300 / 1200) = 1.189207115 [PIL 1.189]
2^((4 × 301) / 1200) = 2.00462632368
2^((4 × 300) / 1200) = 2 PIL
2^(1 / 301) = 1.00230546807 PIL
1.00230546807 × log(523.24 ÷ 261.62) ÷ log(2) = 1.00230546807 PIL
Sea:
2^(1 / 300) = 1.00231316184 | 2^(1/300) × 261.62 = 262.225169401 [C4 + 4 c]
2^(300 / 300) = 2 | 2^(300 / 300) × 261.62 = 523.24
Nuestro “espacio Sauveur” sonopoiético
[ 3.61235994797 ^ (((1200 / 12) * 43) / 1200)) = 99.71285454 PIL ]
99.712885454 ^ (43/43) * 32.703 Hz = 3260.910493 Hz [G7 + 68 ∆]
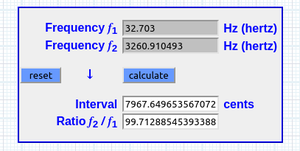
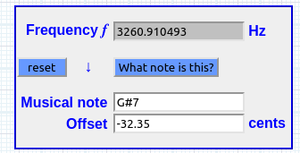
7967.649653567072 ÷ 43 = 185.29417799 (185 ∆)

COROLARIO
log(2) = 0.30102999566 PIL
0.30102999566 ^ (((1200 / 12) * 12) / 1200)) * 261.62 = 78.7554674646 Hz [C# 2 + 22 cents]
log(2) * 12 = 3.61235994797 PIL
Apuntes para el Sauveur (*) exponencial
log(2) = 0.30102999566 (*) PIL→[producto del indice logarítmico del substrato armónico]
Observación : 1er armónico del despliegue SAUVEUR equivalente a la frecuencia 1.301 Hz
[K 0.301]
1 Hz + 301 = 0 ∆
1.301 Hz + 301 = 456 ∆
1.602 Hz + 301 = 816 ∆
1.903 Hz + 301 = 1114 ∆
/////////
2.204 Hz + 301 = 1368 ∆
2.505 Hz + 301 = 1590 ∆
2.806 Hz + 301 = 1786 ∆
////////
3.107 Hz + 301 = 1963 ∆
3.408 Hz + 301 = 2123 ∆
3.709 Hz + 301 = 2269 ∆
////////
4.01 Hz + 301 = 2404 ∆
Realidad material sonora
261.62 * 0.301 = 78.74762 (compromiso 78,75 Hz)
1200 * log2(78.75 / 261.62) = -2078.54520695 ∆
DESPLIEGUE frecuencial
261.62 * 0.301= 78.74762 [substrato armónico (k)]
261.62 Hz [0 ∆]
1) 261.62 + 78.74762 = 340.36762 Hz ~ (1200 * log(340.36762 / 261.62)) / log(2) = 455.545154467 [456 ∆]
2) 340.36762 + 78.74762 = 419.11524 Hz ~ (1200 * log(419.11524 / 261.62)) / log(2) = 815.848977296 [816 ∆]
3) 419.11524 + 78.74762 = 497.86286 Hz ~ (1200 * log(497.82286 / 261.62)) / log(2) = 1113.7915751 [1114 ∆]
4) 497.86286 + 78.74762 = 576.61048 Hz ~ (1200 * log(576.61048 / 261.62)) / log(2) = 1368.14906869 [1368 ∆]
5) 576.61048 + 78.74762 = 655.3581 Hz ~ (1200 * log(655.3581 / 261.62)) / log(2) = 1589.7727241 [1590 ∆]
6) 655.3581 + 78.74762 = 734.10572 Hz ~ (1200 * log(734.10572 / 261.62)) / log(2) = 1786.21801075 [1786 ∆]
7) 734.1081 + 78.74762 = 812.85572 Hz ~ (1200 * log(812.85572 / 261.62)) / log(2) = 1962.6317587 [1963 ∆]
8) 812.85572 + 78.74762 = 891.60334 Hz ~ (1200 * log( 891.60334 / 261.62)) / log(2) = 2122.71502395 [2123 ∆]
9) 891.60334 + 78.74762 = 970.35096 Hz ~ (1200 * log( 970.35096 / 261.62)) / log(2) = 2269.24056765 [2269 ∆]
10) 970.35096 + 78.74762 = 1049.09858 Hz ~ (1200 * log( 1049.09858 / 261.62)) / log(2) = 2404.32661152 [2404 ∆]
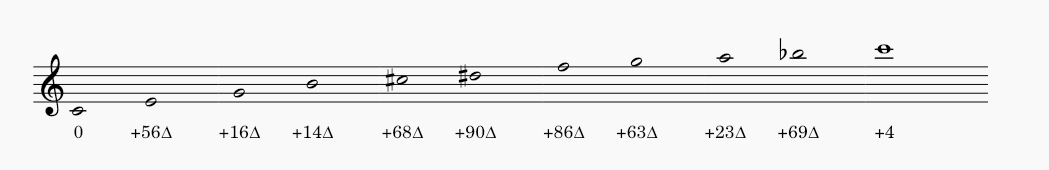
Especulación aritmética
LA FRECUENCIA COMO ESPACIO
261.62 / 300 = 0.87206666666 PIL (Producto Índice Logarítmico)
261.62 * 0.87206666666 = 228.150081332 Hz
f° * PIL = constante frecuencial (K)
I. 261.62 + 228.150081332 = 489.770081332 Hz ~ (1200 * log( 489.770081332 / 261.62)) / log(2)
=1085.55817444 → 1086 ∆ [Bb4 + 86 ∆]
II. 228.150081332 + 261.62= 717.920162664 Hz ~ (1200 * log(717.920162664 / 261.62)) / log(2)
= 1747.62069792 → 1748 ∆ [F5 + 48 ∆]
III. 228.150081332 + 717.920162664 = 946.070243996 Hz ~ (1200 * log(946.070243996 / 261.62)) / log(2)
= 2225.36936474 → 2225 ∆ [Bb5 + 25 ∆]
IV. 228.150081332 + 946.070243996 = 1174.22032533 Hz ~ (1200 * log(1174.22032533 / 261.62)) / log(2)
=2599.39007403 → 2599 ∆ [C#6 + 99 ∆]
V. 228.150081332 + 1174.22032533 = 1402.37040666 Hz ~ (1200 * log(1402.37040666 / 261.62)) / log(2)
= 2906.78726127→ 2907 ∆ [F6 + 7 ∆]
↓
↓
↓
A piacere…
Aclaratoria
El numero 300 corresponde a las 7 heptaméridas * 43 méridas de Joseph SAUVEUR: que por razones de convención operacional asumimos como un compromiso.
Por otra parte, nuestro empleo de la frecuencia C4 es de índole transitoria.
Dicho de otra manera, la utilización de una frecuencia distinta a la evocada, no cambiaría en absoluto el resultado de las proporciones surgidas (tanto en cents como en hercios) aparecidas en la presente especulación.
VARIANTE O REDUCCIÓN ESPACIAL ASOCIADA A LOS CENTS (∆)
Una escala exponencial
(300 * log( 489.770081332 / 261.62)) / log(2) = 271.389543609 → 271 ∆ [D4 + 71 ∆]
(300 * log(717.920162664 / 261.62)) / log(2) = 436.905174481 → 437 ∆ [E4 + 37 ∆]
(300 * log( 946.070243996 / 261.62)) / log(2) = 556.342341186 → 556 ∆ [F4 + 56 ∆]
(300 * log( 1174.22032533 / 261.62)) / log(2) = 649.847518508→ 650 ∆
(300 * log( 1402.37040666 / 261.62)) / log(2) = 726.696815318 → 727 ∆
Y así, hasta el recorrido deseado
Déconstruction : La quête de la hauteur de sons
Vínculos complementarios
L’8ve et “Le tyran UT” ! Consonance ? Tempérament ? Gamme naturelle ? …
Hibridación
