
Apuntes para un folleto interactivo (contribución)
diciembre 2022 / abril 2023
Exordio
En la primera publicación de nuestra serie Los cuadernos abiertos 2019, anunciábamos la futura aparición de un “conjunto de herramientas” ‒próximas a transitar el ciberespacio‒ y concebidas en una “perspectiva múltiple” e inesperada.
Efectivamente, se trata de una cantidad de aplicaciones elaboradas y abiertas fundamentalmente hacia un universo sonoro infinitesimal “quasi inexplorado”: sobre todo, en su “carácter hermenéutico y de pertinencia tecnológica”.
Así, la maquinaria evocada, reúne (a nuestro parecer), el criterio de permeabilidad conciliable con la “díada recursiva” saberes/técnicas, técnicas/saberes ‒tan necesaria en las investigaciones de índole transdisciplinaria e interesadas por los fenómenos estéticos sonoros tanto europeos como no-europeos.
Demos entonces la bienvenida a ese conjunto de herramientas que constituye el ESCALADOR
La autoría corresponde al compositor e investigador Oswaldo González.
La presente investigación, consistirá en situarnos como usuarios preocupados por una dialógica maquínica de índole instructiva y proliferante; orientada hacia la articulación de un laboratorio de preguntas y respuestas concebidas a su vez como una coreografía de saberes y decisiones ‒que interrogan a menudo, la invención, la investigación, la pedagogía, etc.
En lo concerniente al circuito de entretejidos o hipervínculos (responsable y generador de una cierta “idea laberíntica”) ‒a veces incomprensible a primera aproximación‒, se vuelve fecunda al familiarizarse con los mecanismos de interacción del principio extrapolado de “autopoiesis”.
Por lo demás, los procedimientos de cálculo y análisis que se revelan a largo del presente escrito, son apenas algunas de las posibilidades operacionales de lo que el ESCALADOR /CALCULADOR es capaz de procesar.
En fin, corresponderá al usuario interesado de construir la singularidad de sus propias interrogaciones…
log(2) = 0.30102999566 (*) PIL→[producto del indice logarítmico del substrato armónico]
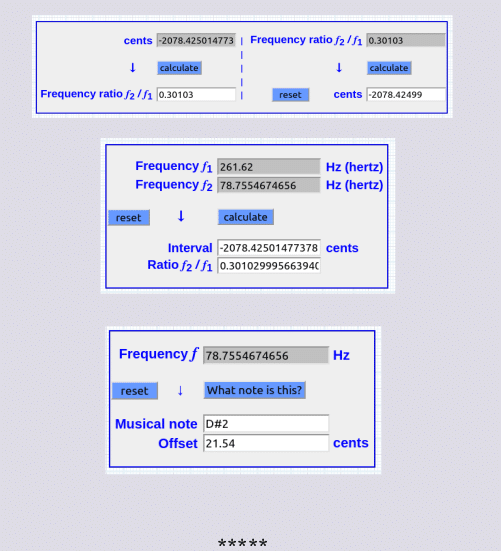
261.62 * 0.301 = 78.74762 (compromiso 78,75 Hz)
1200 * log2(78.75 / 261.62) = -2078.54520695 ∆
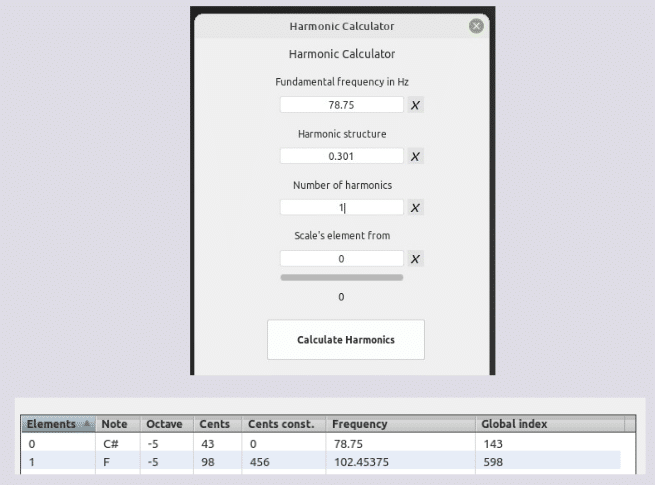
Observación : 1er armónico de SAUVEUR equivalente a la frecuencia 1.301 Hz
Operación frecuencia
[K 0.301] HS
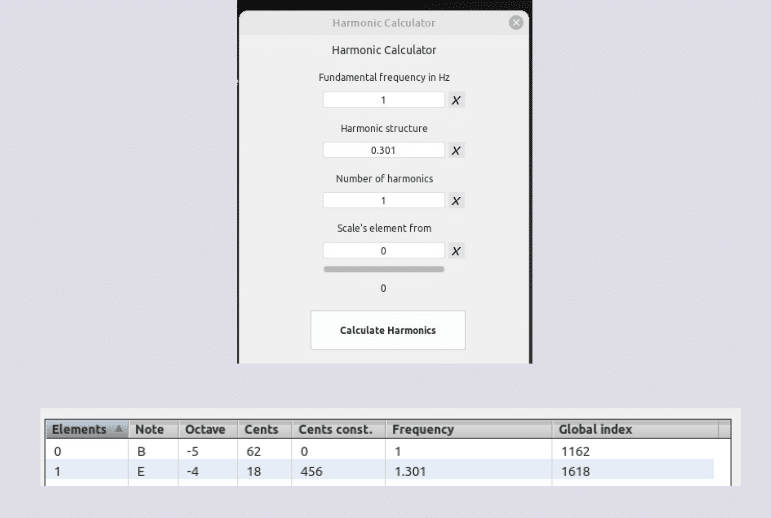
1.301 ~ 1Hz + 301
1.602+ 301
1.903+ 301
/////////
2.204+ 301
2.505+ 301
2.806+ 301
////////
3.107+ 301
Verificación
La observación precedente, nos conduce a postular heurísticamente el empleo de un “substrato armónico” como la
constante operacional (K) en su despliegue exponencial:
Ejemplo con substrato original:
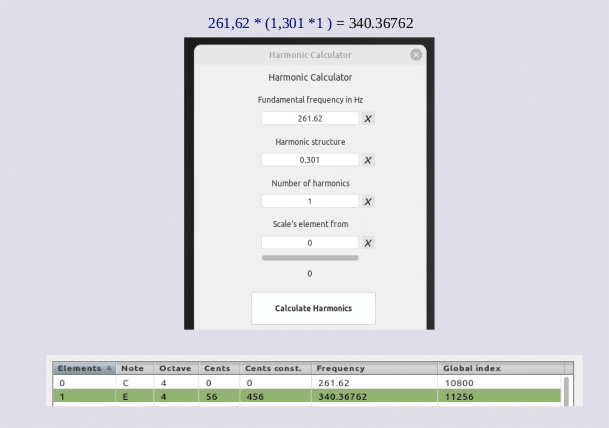
261.62 * 0.301 = 78.74762 [substrato armónico (k)]

0) 261.62
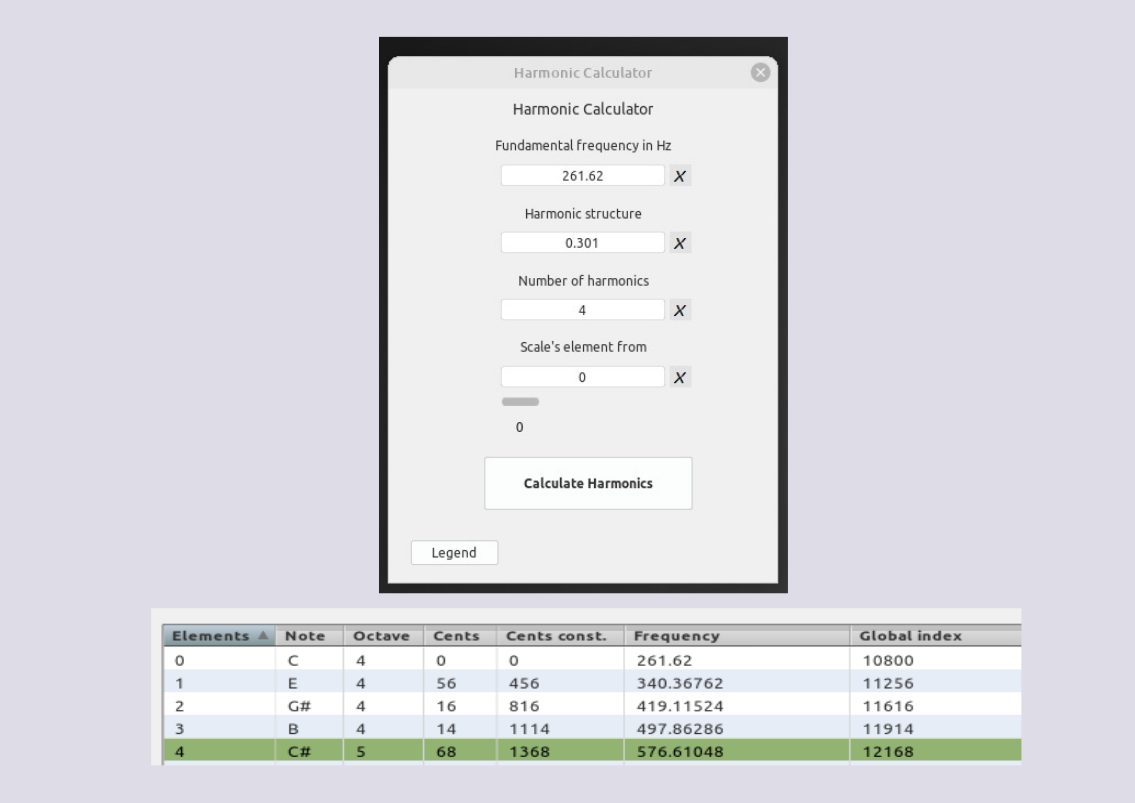
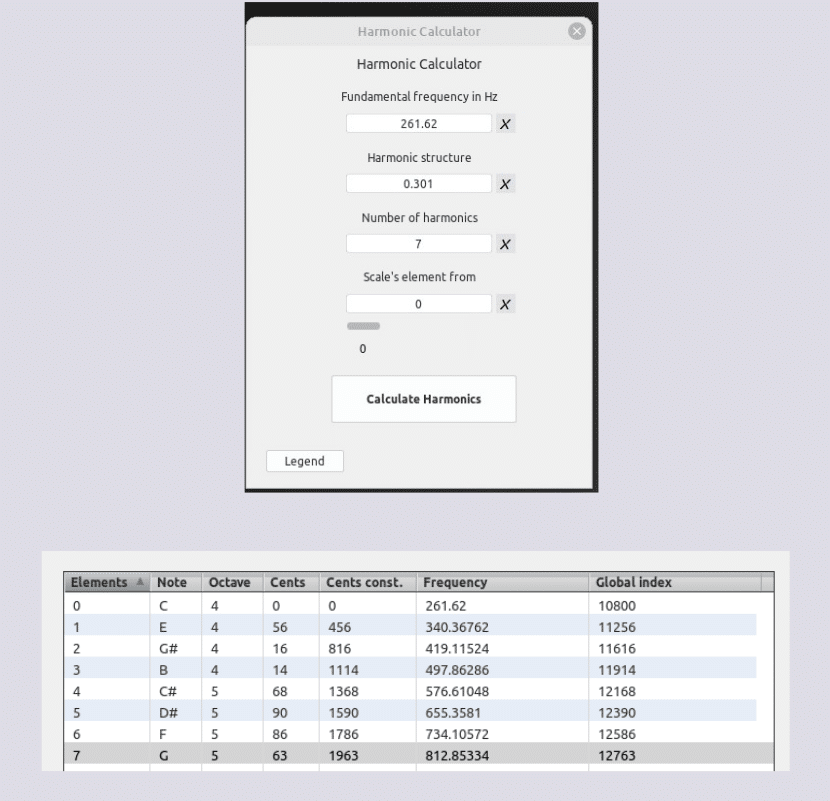
1) 261.62 + 78.74762 = 340.36762
2) 340.36762 + 78.74762 = 419.11524
3) 419.11524 + 78.74762 = 497.86286
4) 497.86286 + 78.74762 = 576.61048
5) 576.61048 + 78.74762 = 655.3581
6) 655.3581 + 78.74762 = 734.10572
7) 734.1081 + 78.74762 = 812.85572
8) 812.85572 + 78.74762 = 891.60334
9) 891.60334 + 78.74762 = 970.35096
10) 970.35096 + 78.74762 = 1049.09858
Recursividad dialógica / link (Sengpielaudio)
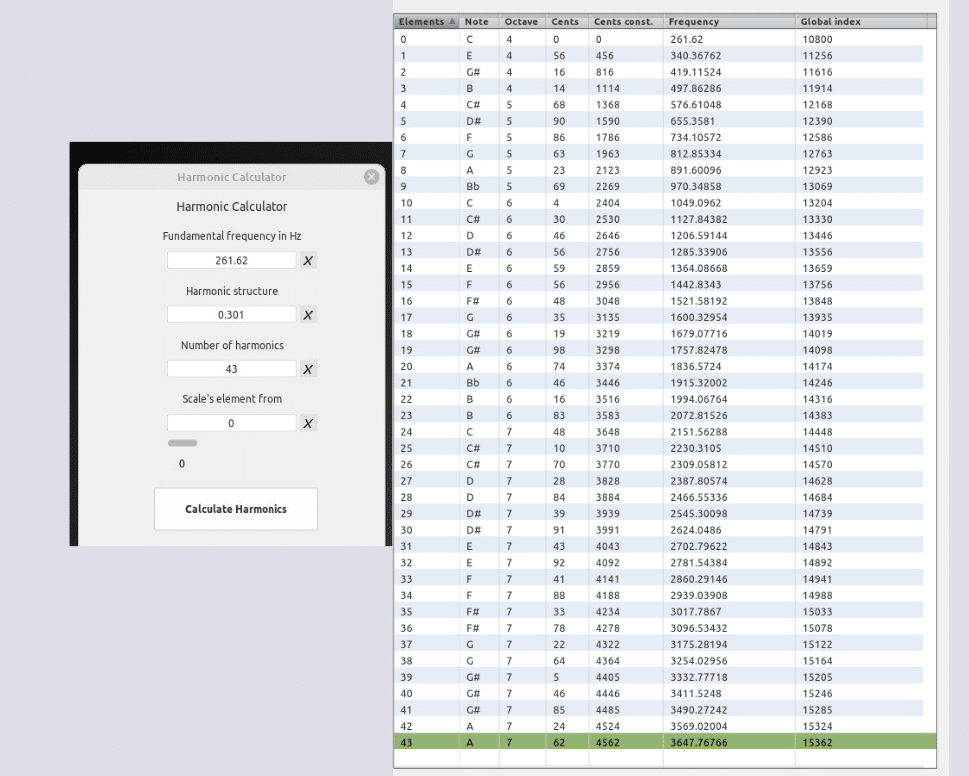
Secuencia: 1 – 4 – 7 – 28 – 43 – 300
Constante proliferante (1)
Primer segmento exponencial de las heptaméridas
(4) / 28m ÷ 7hpm = 4
Segundo segmento exponencial heptaméridas (7) / 300 ÷ 43
Constante proliferante exponencial (28) / 7 * 4
261.62 + (Kp * Ea)
(Kp) constante proliferante
(Ea) escala armónica
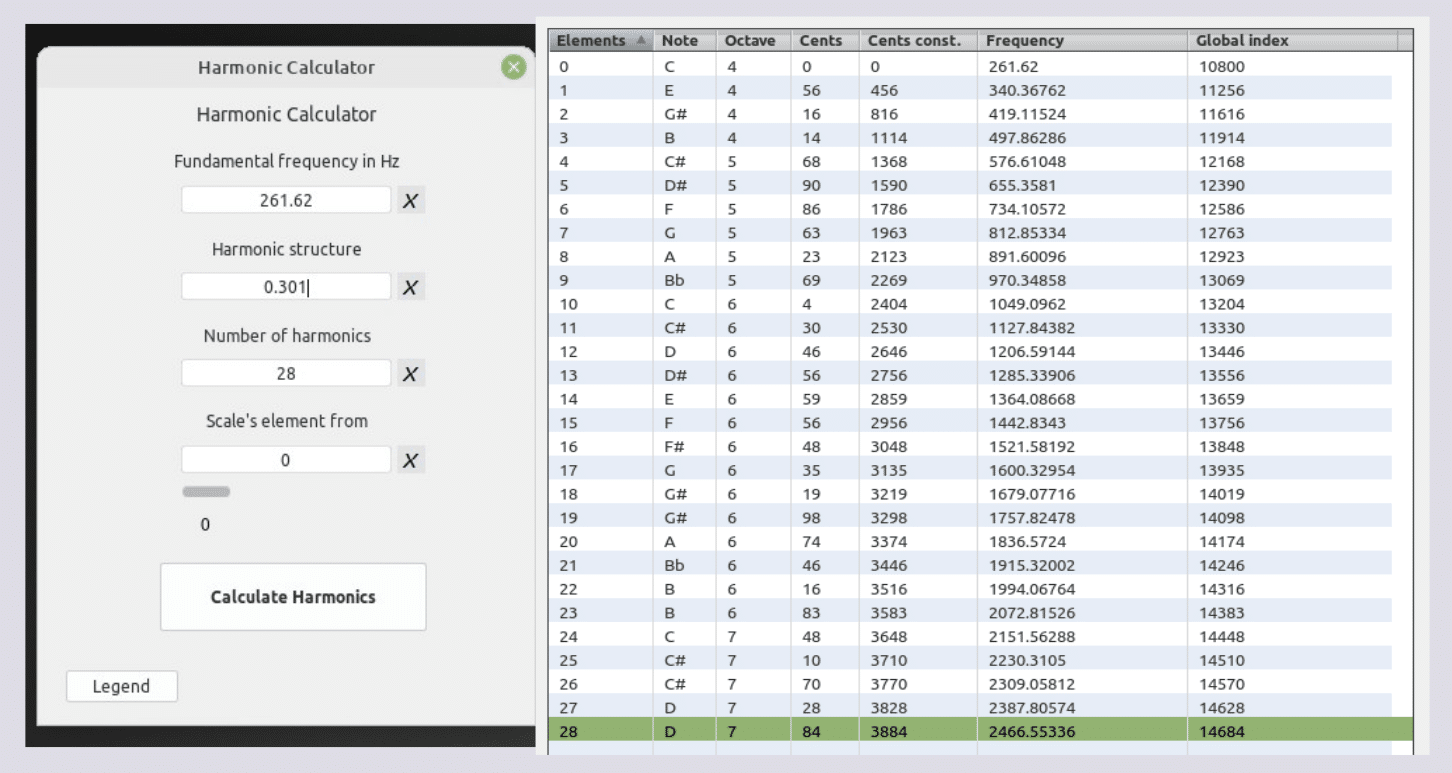
Despliegue del conjunto armónico de méridas (43)
Adaptación tesitural

La constante frecuencial potencializada *
El sonido rector substrato de un despliegue armónico
log(2) * 261.62 = 78.7554674656 Hz
Procedimientos logarítmicos para los Sauveurs
Log(2) = 0.30102999566
log(2) * 261.62 = 78.7554674656 Hz (78.75 D#2 + 21.42 ∆)
1200 * log2(78.75 / 261.62) = -2078.54520695 ∆ , sea:
↓
340.36762 + 78.75 = 419.11762
419.11762 + 78.75 = 497.86762
497.86762 + 78.75 = 576.61762
576.61762 + 78.75 = 655.36762
655.36762 + 78.75 = 734.11762
734.11762 + 78.75 = 812.86762
812.86762 + 78.75 = 891.61762
891.61762 + 78.75 = 970.36762
970.36762 + 78.75 =1049.11762

↑
(1049.0962 Hz) – (970.34858 Hz) = 78.74762 Hz
(970.34858 Hz) – (891.60096 Hz) = 78.74762 Hz
(891.60096 Hz) – (812.85334 Hz) = 78.74762 Hz
(812.85334 Hz) – (734.10572 Hz) = 78.74762 Hz
(734.10572 Hz) – (655.3581 Hz) = 78.74762 Hz
(655.3581 Hz) – (576.61048 Hz) = 78.74762 Hz
(970.34858 Hz) – (891.60096 Hz) = 78.74762 Hz
(497.86286Hz) – (419.11524Hz) = 78.74762 Hz
(419.115424 Hz) – (340.36762 Hz) = 78.747804 Hz
(340.36762 Hz) – (261.62 Hz) = 78.74762 Hz

La escala exponencial de Sauveurs (300)
[cromatismo “exponencial” frecuencial]
(lista de 256 a 300)
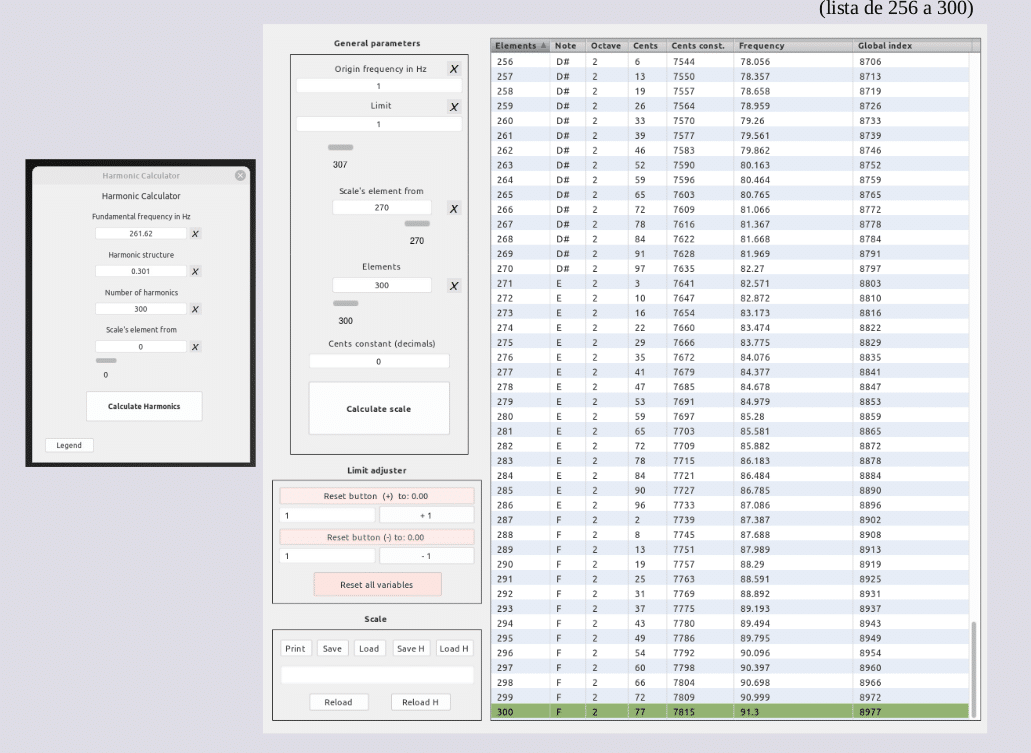
Recordatorio
la 8va de Méridas (1200÷4)
Y Finalmente, un modo octavante Sauveur
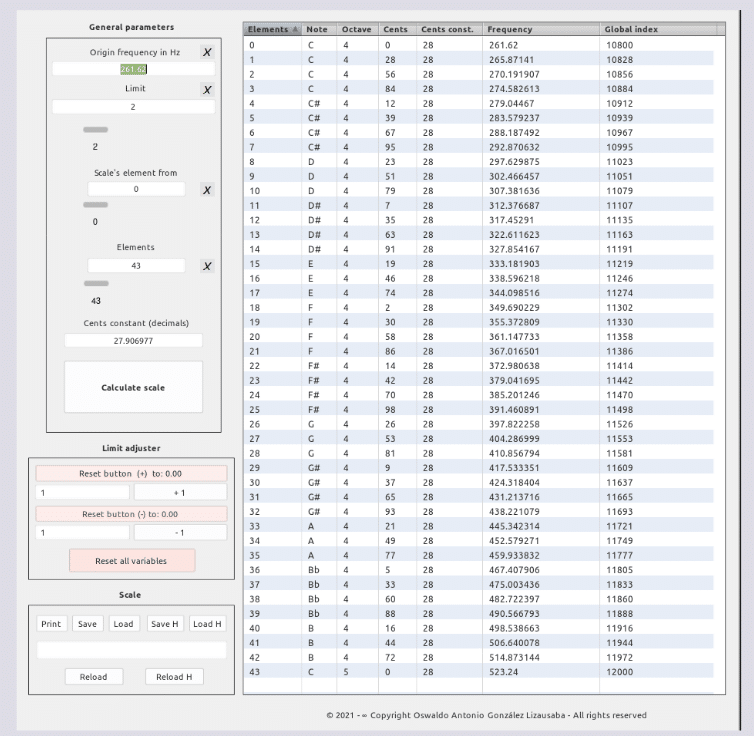
Parámetros Escalador
LIMIT : 2
ELEMENTS: 7

LA TRADICIÓN
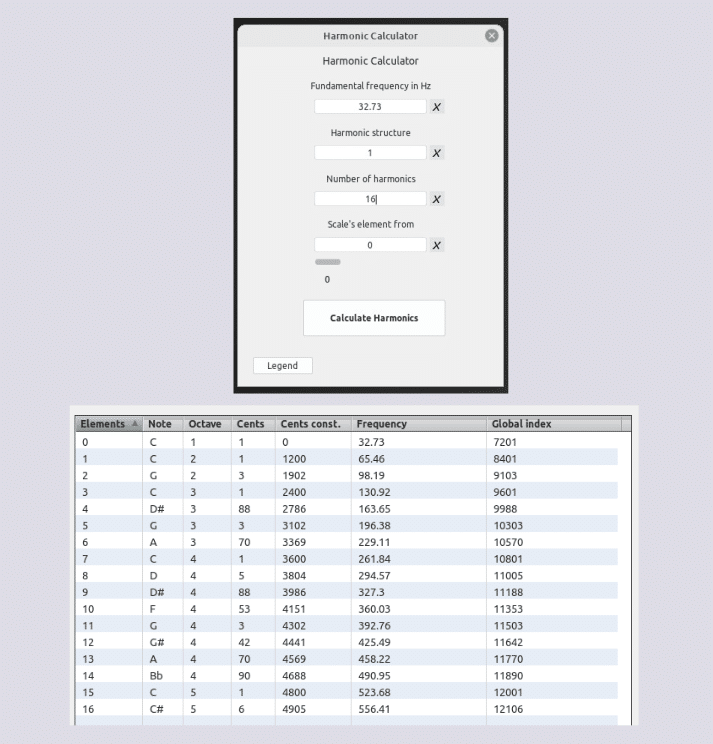
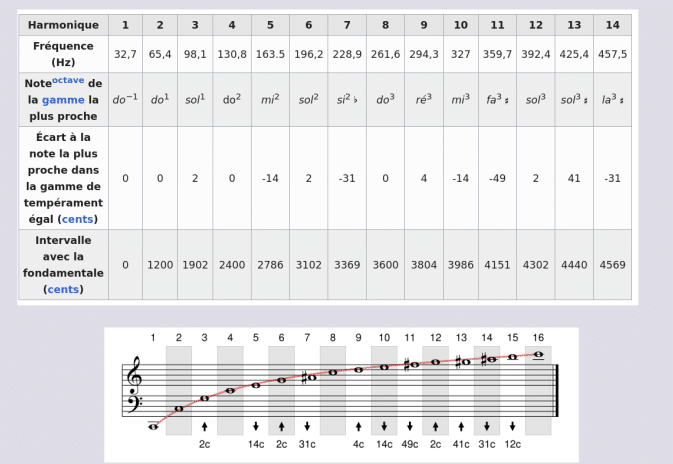
Fuente https://en.wikipedia.org/wiki/Harmonic
Anexos
LÍMITE / LOGARITMO / PROGRESIÓN
Modo logarítmico de la 8va [Harmonic structure : 0,1] (operación frecuencial multiplicativa)
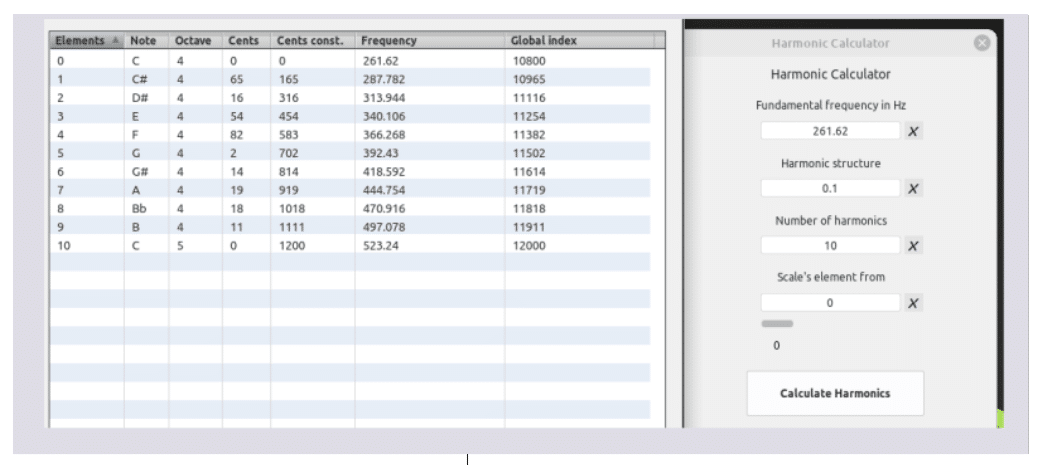
261.62 * 1.1 = 287.782
261.62 * 1.2 = 313.944
261.62 * 1.3 = 340.106
261.62 * 1.4 = 366.268
261.62 * 1.5 = 392.43
261.62 * 1.6 = 418.592
261.62 * 1.7 = 444.754
261.62 * 1.8 = 470.916
261.62 * 1.9 = 497.078
261.62 * 2 = 523.24

El mismo procedimiento: pero esta vez con doce términos y la estructura armónica 0.301
(operación frecuencial aditiva)
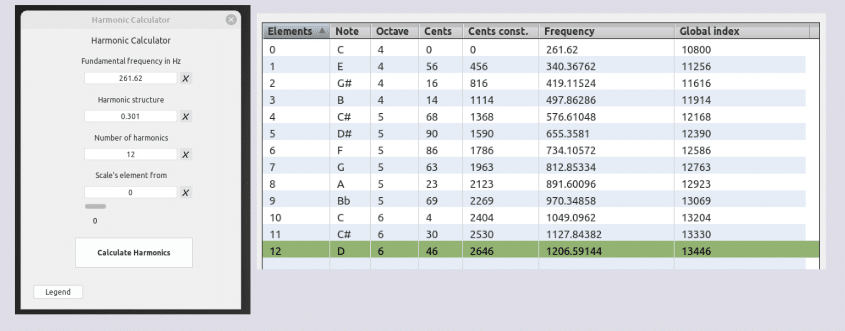
261.62 + 78.74762 = 340.36762 Hz
↓
1127.84382 + 78.74762 = 1206.59144 Hz [X(ava) 2646 ∆]
Invariante metatonal DO – FA – SOL
sonido ausente un nota antípoda FA#

Sobre la METATONALIDAD (es/fr)
Otras proliferaciones
Log(261.62) = 2.41767094133 PIL
(log(261.62) ^ (((1200/1200) * 1200) / 1200)) * 261.62 = 632.511071669 Hz [1528 ∆]
(log(261.62) ^ (((1200/1200) * 1200) / -1200)) * 261.62 = 108.21158311 Hz [-1528]
(log(261.62) ^ (((1200/1200) * 1200) / -1200)) = 0.41362121821 PIL
Un ejemplo operacional
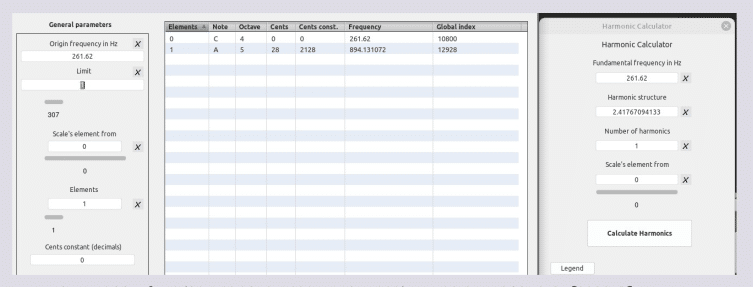
Sea: 1200 * log2(894.131072 / 632.511071669) = 599.274720372 ∆ [°600 ∆]
1528 ∆ + 600 ∆ = 2128 [frontera flotante o “clausura operacional”]
EJEMPLO : MODO LOGARÍTMICO C4
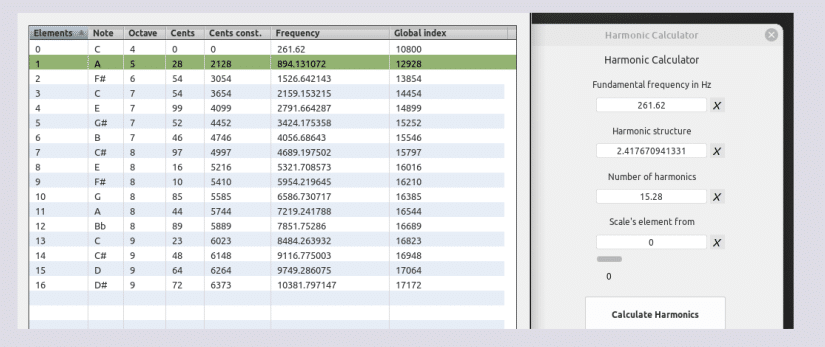

UNA BÚSQUEDA DE ESPACIO NO OCTAVANTE
log(100) ^ (1404 ÷ 1200) = 2.25011696938 PIL
Recorrido global en hercios 2.25011696938 * 261.62 = 588.675601529 Hz ~ 1404 ∆
observación preliminar
Finalmente todo se reduce a
o simplemente a
1404 (espacio) ÷ 18 (términos)
18 * 78 (K) = 1404

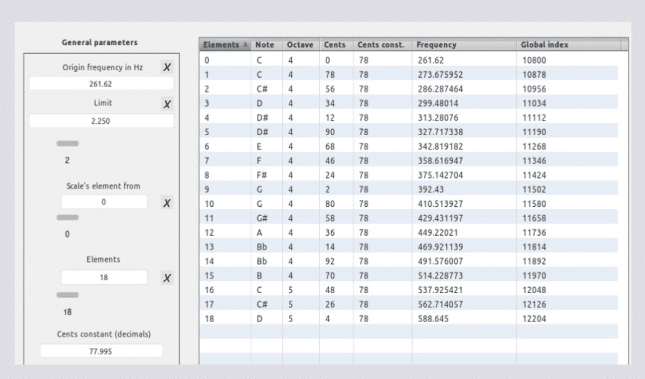

Espacio tesitural
log(100) ^ (1404 * 10 ÷ 1200) = 3326.98581548 PIL
Con 180 elementos
Sea:
1. una frecuencia de origen de 16.352 Hz [C0]
2. un limite de 3326.98581548 PIL
3. un conjunto de 180 términos
4. una constante (K) de 78 ∆
DIALÓGICA DE LA DIALÓGICA
Log(301) =2.47856649559 PIL
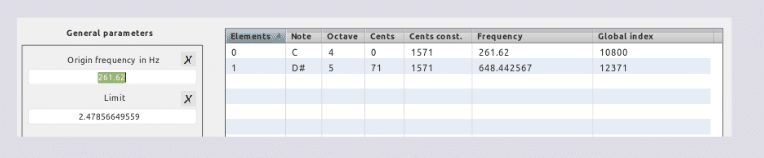
HC
261.62 + 648.442567 = 910.062567 Hz
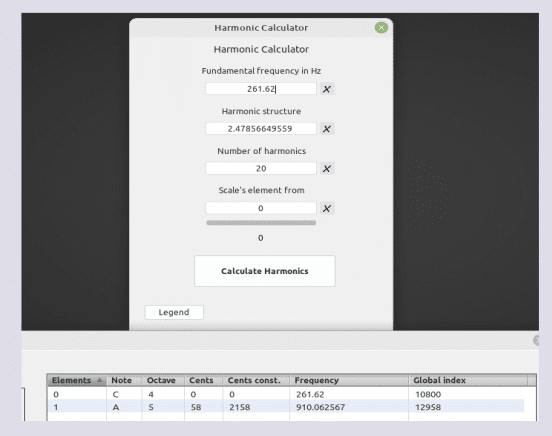
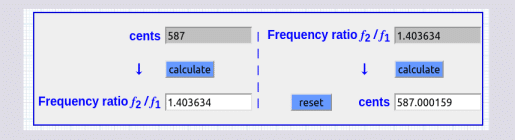
2158-1571 = 587∆ [500 + 87] una 4ta + 87 ∆

Obtenemos así nuestro primer modo logarítmico SAUVEUR
261,62 x 1,00057778950655 ^ 587 = 367.218693282
PIL 1.403634
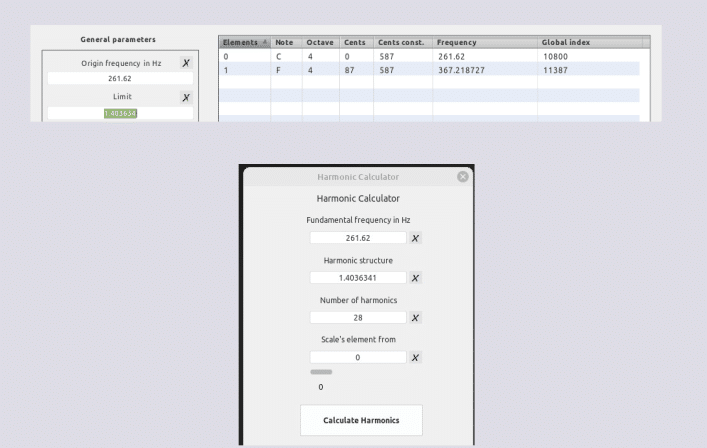
Modo logarítmico Sauveur de 28 términos
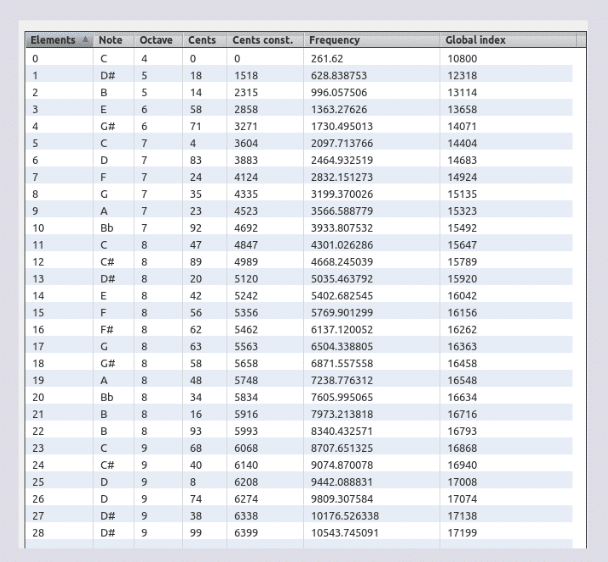
Despliegue tesitural
28 * 1.403634 = 39.301752 PIL
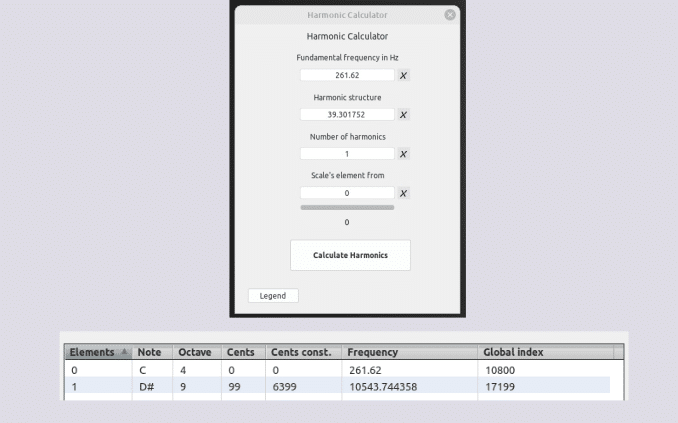
Modo logarítmico Sauveur de 43 términos

43 * 1.403634 = 60.356262 HC
↑
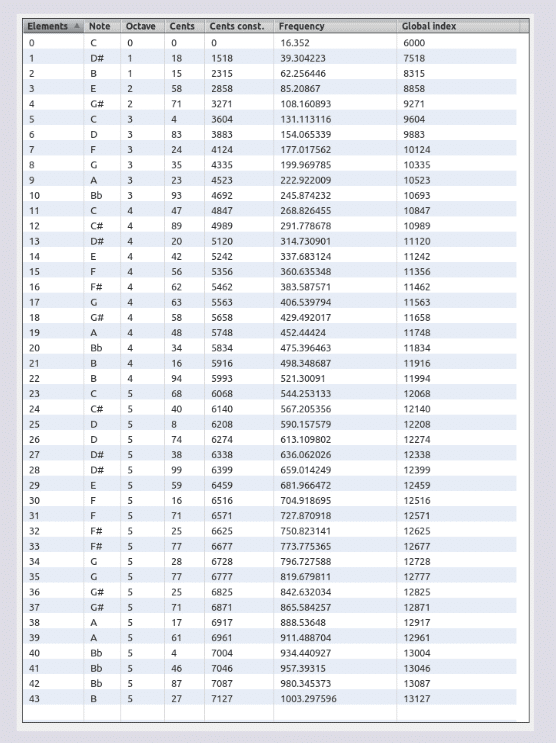
Despliegue tesitural
↓
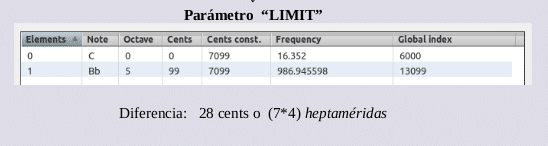
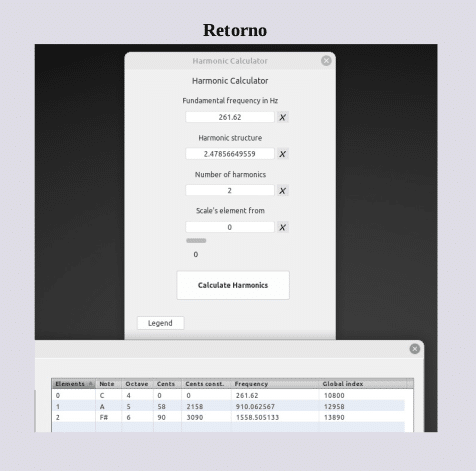
648.442577 + 910.062567 = 1558.505144 Hz
… y así, ¡hasta!…
Por último, algunas preliminares para un despliegue ÁUREO
Procedimientos
ESCALADOR LIMIT : 1.618
K = 833 ∆
833 + 833 = 1666 ∆
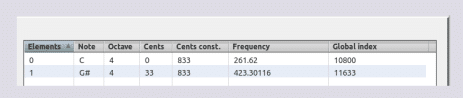
Recursividad/iteración: 261.62 * 1.618 = 423.30116 Hz ~ 833 ∆
sea: 1.618 * 261.62 = 423.30116 Hz
1.618 * 423.30116 = 684.90127688 Hz [E5 +66 ∆ ó F5 -33.92]
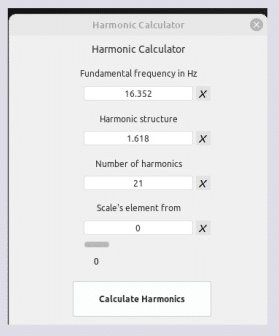
Harmonic Calculator

Verificación: 1666 – 833 = 833
1200 * log( 684.92116 / 261.62) / log(2) =1666.15811674
El 1er armónico de Hc ~ al doble del 1er término de “Escalador Limit”
1666 + 833 = 2499 ∆
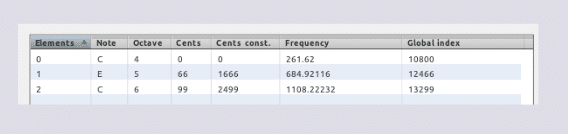
1200 * log( 684.92116 / 261.62) / log(2) + 833 ∆ = 2499.15811674 ∆
ÁUREO 21 términos

Proliferación del PIL en la serie Fibonacci
1, 1, 2, 3 , 5, 8, 13, 21, 34, 55, 144, 233
1+1 = 2
3/2 = 1.5
5/3 = 1.66666666667
8/5 = 1.6
13/8 = 1.625
21/13 = 1.61538461538
34/21 = 1.61904761905
55/34 = 1.61764705882
89/55 = 1.61818181818
144/85 = 1.61797752809
233/144 = 1.61805555556
A partir de la observación precedente y luego de todo nuestro recorrido, nada impide de manera heurística, operar el producto logarítmico del SAUVEUR con el número 1.618:
0.301/1.618 = 0.18603213844 PIL
65.406 Hz [C2] * 0.18603213844 = 12.1676180468 [constante Hz]
Obtenemos así el desplazamiento siguiente:
65.406 + 12.1676180468 =77.5736180468 Hz
77.5736180468 + 12.1676180468 = 89.7412360936 Hz
89.7412360936 + 12.1676180468 =101.90885414 Hz
y así sucesivamente…
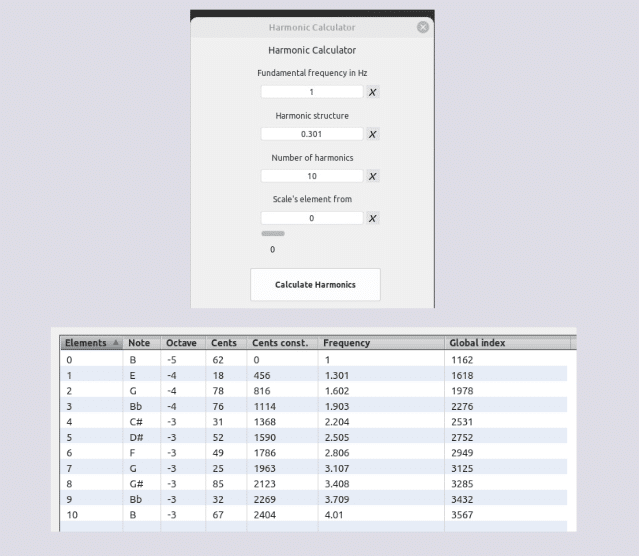
Verifiquemos la “operacionalización”
en Harmonic Calculator
(8 primeros términos de la sucesión Fibonacci)


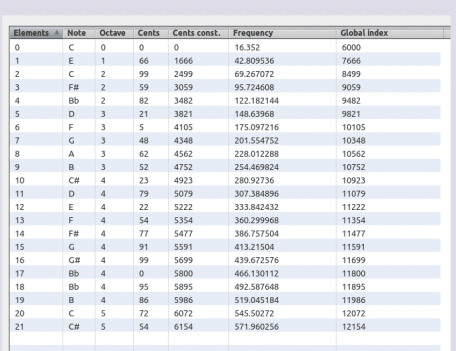
Ciclo armónico de méridas (43 términos) Sauveur/Fibonacci
⇓
Vertimiento semántico o singularidad de nuestra interrogación
Corolario
0,301 / 1,618 ~ 0.18603213844 [PIL]
65.406 Hz * 0.18603213844 ~12.1676180468 Hz
Sea: 65.406 +12.1676180468 Hz ~ 77.5736180468 Hz
ó
65.406 * 0.18603213844 + 65.406 ~ 77.5736180468 (C2 + 0∆ → lista Escalador n°1)
↓
77.5736180468 + 12.1676180468 ~ 89.7412360936 Hz
ó
Sea: 65.406 * 0.18603213844 + 77.5736180468 ~ 89.7412360936 (F2 + 48∆ → lista Escalador n°2)
Modo Fibonacci en cents por operacionalización
o la búsqueda de un sentido


La Equisava (Xva)
vertimiento semántico & logaritmo
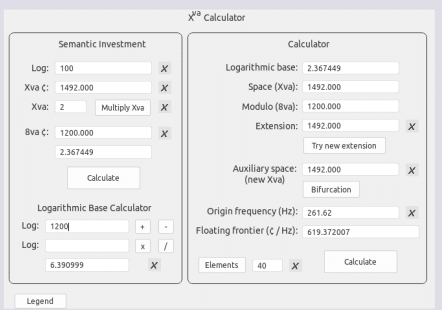
Ejemplo de Dialógica Sonoiética
Henos finalmente en el punto de quiebre de la preocupación fundamental −que acompaña desde el alba de siglo XX (e incluso desde mucho antes) el conflictivo postulado referente a la “emancipación de la 8va”−y que la Sonocreatica preferiría denominar la “deconstrucción” de la misma.
En efecto, las investigaciones teóricas y compositivas de Julián CARILLO 1875-1965 (Sonido 13) y el espectacular y laborioso proyecto en torno a los imaginarios sonoros en el pensamiento occidental de Ivan WYSCHNEGRADSKY / 1893-1979, marcaran para siempre “un no retorno” a ese obscurantismo institucional seudocientífico en los imaginarios sonoros y por consiguiente, en los imaginarios estéticos (…y esta vez a escala planetaria).
Ciertamente, la reflexión sobre la problemática evocada no se detiene a dos autores pilares. De hecho,a lo largo del siglo 20 y de lo que ha transcurrido del presente, compositores, musicólogos, etnomusicólogos y por supuesto, el advenimiento de la informática moderna −que sin contesta es tributaria del Ábaco chino, de los trabajos de Blaise PASCAL, G. LEIBNITZ, Charles BABBAGE, etc, se han abocado (a veces con aciertos y otras, de manera imprecisa) a las implicaciones filosóficas, históricas y sobre todo hermenéuticas de la TÉKNE (*) que la problemática evocada impone.
Por nuestra parte, tan sólo diríamos que la OCTAVA se puede asociar a un recorrido; que por ser recorrido revela un espacio y el mismo, una magnitud.
Ahora bien, si aceptamos este postulado, suponemos entonces que la magnitud en cuestión, agrupa en su constitución “substrato” espacios aún más pequeños ‒que justifican ineludiblemente su suprema presencia.
Surgen así (en su constitución escalística), dos categorías capitales: por un lado, un espacio depositario global de doce sonidos, y por el otro, un espacio de proliferación local ‒conocido universalmente por todo músico como el semitono cromático.
Esto nos conduce a formular que una emancipación de la 8va supone la identificación y deconstrucción de los máximos y mínimos absolutos que han legitimado su hegemonía apodíctica.
Comencemos entonces por definir una equis(ava) Xva

Un postulado para las equisavas
Una vez definida la deconstrucción, aclaremos el sentido que le damos al “vertimiento semántico”. En una expresión tan corta como el término que la origina, un vertimiento semántico no es más que una significación del proceso deseado.
Es por ello que en nuestro proceder de interaccion dialógica todos los operadores aritméticos básicos que se encuentran solicitados, necesitan de la valoración evocada: y tal valoración (en nuestro caso), la obtenemos desde el ángulo que se genera la interrogación.
Así, los resultados aritméticos sin vertimiento, no pueden ser más que absolutos y desprovistos de sentido creativo.
Mínimas et Máximas de una constante (K)
Corolario para una interrogación de la Recursividad Hz / ∆ (cents)
Dado que la constantes mínimas y máximas de una 8va temperada nos remiten a los números 1 y 12 (semitono cromático (+) conjunto de doce grados de la escala respectivamente), la misma observación equivale a los números 100 y 1200 −que señalan el recorrido de 100 ∆ sobre 12 términos = 1200 cents (∆).
Ahora bien, puesto que se trata de una transformación del espacio de la 8 va (1200 ∆ /12 términos) o si preferimos (100 ∆ * 12 términos), imaginemos el emerger de una “mínima” espacio local distinta al espacio global “máxima” que deseamos transformar.
Escojamos completamente al azar la cifra 156 como la constante mínima del espacio a emancipar (magnitud de 1200 cents ~ a la 8va)
obtenemos así:
{ 156 * 12 = 1872 ∆ } ~ 1 octava + 672 ∆ (idea deseada)
Vertimiento semántico
(Log(100)^((1872/100) / 12)) * 261.62 = 771.396625255 [Xave]
Sea: 1872 ∆ para el recorrido

[F#5 + 72 ∆]
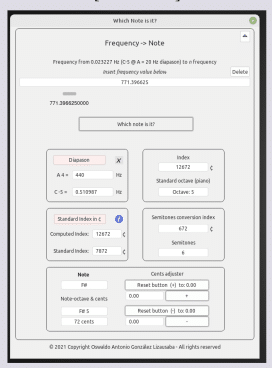
ossia
(2^(18.72 / 12)) * 261.62 = 771.396625255 Hz
Ratio:
771.396625255 / 261.62 = 2.94853843458 PIL
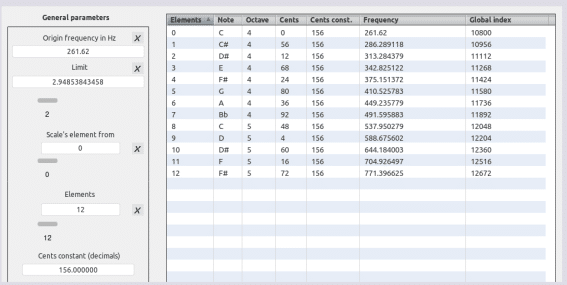

Ciclos espaciales de la equis(ava) 1872
2^(((1872 × 8) /100) / 12)) = 5712.87005737 PIL
5712.87005737 PIL × 16.352 Hz [C0] = 93416.8511781 Hz [F12 + 6 ∆]
Recursividad
93416.8511781 ÷ 16.352 [C0] = 5712.87005737
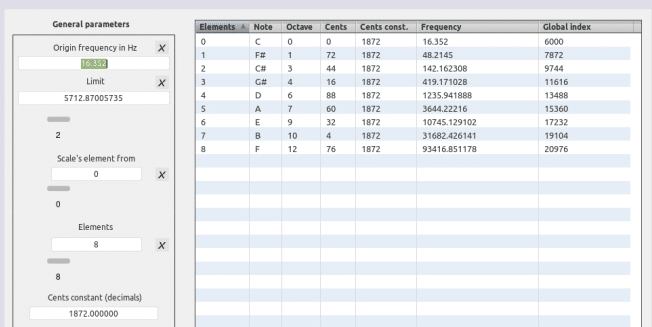
Recorrido (tesitura) : 2 – 4 – 8 – 16 – 32 – 64 -128 – 256 – 512…
(2^((1200/100) / 12)) * 261.62 = 523.24 Hz [C5]
(2^((1200/100) / 12)) × 261.62 × 32 = 16743.68 Hz [C10]
(2^((1200/100) / 12)) × 16,352 [C0] × 512 = 16744.448 Hz [C10]
1492
La “Enacción“de un espacio
Log(1492) * Log(1200) = 9.77260943949
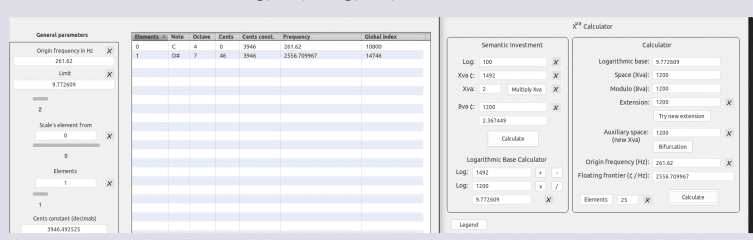
Una extrapolación
1/4 de 1492
24 términos
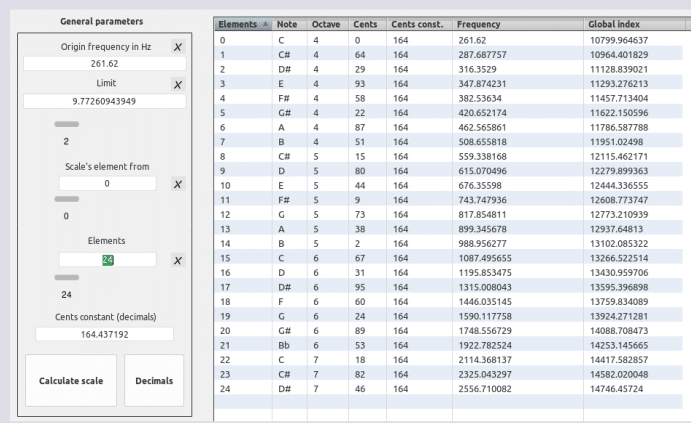
X(ava) 1492 & Sauveur
log(2) = 0.30102999566 PIL →[producto del indice logarítmico del substrato armónico]
261.62 * 0.301 = 78.74762 (compromiso 78,75 Hz)
1492 * log2(78.75 / 261.62) = -2584.32454064 ∆
1492 * log2(261.62 / 78.75) = 2584.32454064
Verificación
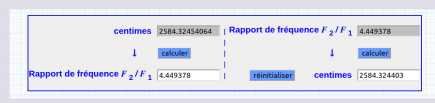
Sauveur ⇔ cents ⇔ X(ava) ~ 4.449378 PIL

Adaptación tesitural
HC 1492 hibridación
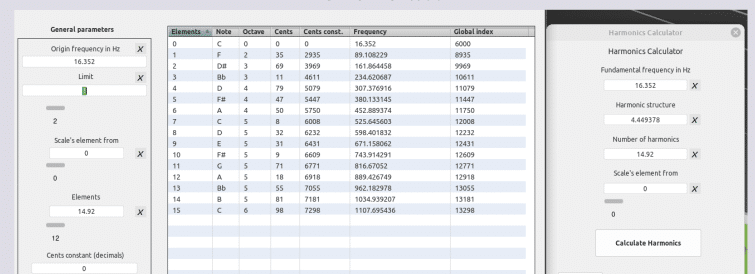

Lecturas complementarias
Yuxtaposición de recorridos espaciales
No podemos clausurar el presente escrito sin señalar una vez más que los resultados aritméticos obtenidos en nuestro procedimiento dialógico (por ser absolutos) necesitan y necesitaran siempre, de la valoración de un vertimiento semántico inicial: una singularidad de nuestras interrogaciones…
COROLARIO
Síntesis de la síntesis
Logaritmo (log), diapason (♪) , Xave , fréquence (f°) & despliegue armónico
log(100) = 2
***
log(100) ^ ((((-900) / 1200) * 1200) / 1200)) * 440 = 261.625565301 Hz [C4 ♪440]
log(100) ^ ((((-900) / 1200) * 1200) / 1200)) * 432 = 256.868736841 Hz [C4 ♪432] Link ⇒
***
log(100) ^ ((((1200) / 1200) * 1300) / 1200)) * 261.62 = 554.353469493 Hz [C#5]
log(100) ^ ((((1200) / 1200) * 1492) / 1200)) * 261.62 = 619.37200141 Hz [C D5 + 91∆]
log(100) ^ ((((1200) / 1200) * 1492) / 1200)) = 2.36744897718 PIL
***
log(100) ^ ((((100) / 1200) * 1200) / 1200)) * 261.62 =C#4 … log(100) ^ ((((1200) / 1200) * 1200) / 1200)) * 261.62 = C5
***
log(2) = 0.30102999566 [PIL]
261.62 * 0.301 = 78.74762 Hz
1) 261.62 + 78.74762 = 340.36762
2), 3), 4), 5), 6), 7), 8), 9),
↓
10) 970.35096 + 78.74762 = 1049.09858
etc.,
Diapasón – ESCALADOR – Operaciones
Anexo J. Sauveur
Déconstruction : La quête de la hauteur de sons
FIN
Los ejemplos de las partituras con sus respectivos audios,
fueron realizados en MuseScore 3.6.2
Para los cálculos adicionales :
Google calculator – Sengpielaudio – Hyperphysics
Texto fundamental (es) 1937 A. E. SAGASTUME BERRA

