Aide-mémoire

por

Un calcul heuristique

[Hertz – Cents – Sauveur – Savart – Octave – X(aves) – Midicents, etc…]

Google calculatrice

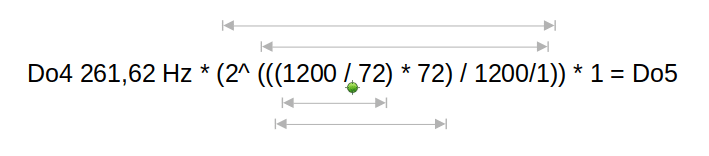
L’héritage de Wyschnégradsky

(((1200 log(880hz/440hz)) / log(2)) / 72 * 1 = 16.6666666667 = La1/12ème

La gamme chromatique

DO4   261,63 * 2^(0/12) |  Do# 261,63 * 2^(1/12)    | Ré      261,63 * 2^(2/12)

Mib   261,63 * 2^(3/12)  |  MI   261,63 * 2^(4/12)   | Fa       261,63 * 2^(5/12)

Fa#    261,63 * 2^(6/12)  |  SOL 261,63 * 2^(7/12)   | SOL#  261,63 * 2^(8/12)

La     261,63 * 2^(9/12)   |  Sib 261,63 * 2^(10/12)   |  Si        261,63 * 2^(11/12)

Do5 261,63 * 2^(12/12) (8ve)

Déploiement des harmoniques

Do2 32,703 * 2^((1200 / 12) * 0)) * 1 | Do2 32,703 * 2^((1200 / 12) * 0)) * 2

Do2 32,703 * 2^((1200 / 12) * 0)) * 3  | Do2 32,703 * 2^((1200 / 12) * 0)) * 4

Do2 32,703 * 2^((1200 / 12) * 0)) * 5  | Do2 32,703 * 2^((1200 / 12) * 0)) * 6

Do2 32,703 * 2^((1200 / 12) * 0)) * 7   | Do2 32,703 * 2^((1200 / 12) * 0)) * 8

   Do2 32,703 * 2^((1200 / 12) * 0)) * 9    | Do2 32,703 * 2^((1200 / 12) * 0)) * 10

  Do2 32,703 * 2^((1200 / 12) * 0)) * 11 | Do2 32,703 * 2^((1200 / 12) * 0)) * 12

   Do2 32,703 * 2^((1200 / 12) * 0)) * 13 | Do2 32,703 * 2^((1200 / 12) * 0)) * 14

    Do2 32,703 * 2^((1200 / 12) * 0)) * 15 | Do2 32,703 * 2^((1200 / 12) * 0)) * 16

Corollaire

                                          /////////////////////////////////////////////////////////////////////////////////////////////////////////////

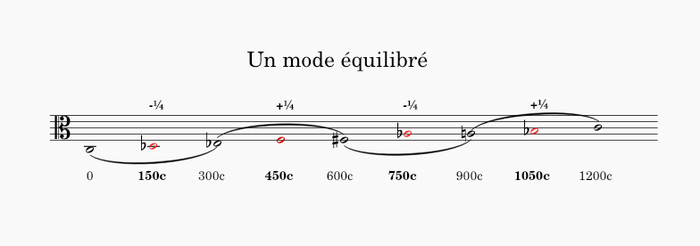
261,63*(2^(1/300)) 1 savart ≡ 1 heptaméride ▶

261,63*(2^(5,5/300)) / (200/9)*1 1ère COMA I ● (22,2222222222)

Hyperphysics cents

261,63*(2^(7/300)) 1ère méride de sauveur ▶

261,63*(2^ (50/300)) Ré4 200 cents

261,63*(2^ (0/300)) Do4 [1,2,3 …… et ainsi jusqu’à (50 cents)

Source

Rappel!

440Hz * 2^ (1/1200) ≃ 440.254227383 (La 1(1 cent) ) soit (1c,2c,3c,…1200c)

Pour en finir :

1 mHz = 0.001 Hz

 

Soit : 261,62 * (2^(((1200 / 1) * 0) / 1200/1)) + 0,1 = 261,72  (Hertz)

/

261,62 * (2^(((1200 / 1) * 0) / 1200/1)) + 0,001 = 261,621   (millihertz) 

Source

QUELQUES REPÈRES POUR UNE IDÉE DE CONCATÉNATION

(mille hertz – hertz – cents)

(440 + (0 / 0.001)) * 2^(1/1200)) ∼ 440.254227383 Hz, soit La + 1 cents

(440 + (0 / 0.001)) * (2^(4/1200)) ∼ 441.017791211 Hz, soit La + 4 cents (1er Savart / Heptaméride)

(440 + (0 / 0.001)) * (2^(16.66/1200)) ∼ 444.254643874 Hz, soit La + 17 cents (1/12) Ivan Wyschnégradsky

(440 + (0 / 0.001)) * (2^(20/1200))   ∼ 445.112553733 Hz, soit La + 20 cents (1/10 d.t)  

(440 + (0 / 0.001)) * (2^(22.22/1200)) ∼ 445.683697596 Hz, soit La ± 22 cents (1er COMA)

(440 + (0 / 0.001)) * (2^(28/1200))  ∼ 447.174170154 Hz, soit La + 28 cents (1er Méride de Sauveur)

(440 + (0 / 0.001)) * (2^(40/1200)) ∼ 450.285 Hz, soit La + 40 cents (1/5 d.t)

(440 + (0 / 0.001)) * (2^(50/1200)) ∼ 452.892984123 Hz, La + 50 cents (1/4 d)

(440 + (0 / 0.001)) * (2^(66.66/1200)) ∼ 457.272298578 Hz, soit La + 66,66 cents (1/6 d.t)

(440 + (0 / 0.001)) * (2^(28.571428571/1200)) ∼ 447.321793332 Hz, soit La + 29 cents (1/7 de ton)

(440 + (0 / 0.001)) * (2^(12/1200)) ∼ 443.060442025 Hz, soit 1er 1/2 ton

Enaction d’une “sonoïèse fréquentielle”

Si le néologisme « sonopoïèse » nous signale le domaine de l’auto-référentialité d’un espace/mouvement sonore à venir, le vocable « sonoïèse » signifiera l’auto-référentialité d’un déploiement fréquentiel à structurer.

 récursivité heuristique 440 + (1/ 3.66666666667) | 440* (2^(10/1200))  ou 440*1,00057778950655 ^ 10

Épigraphe →

lorsqu’un espace se partage en deux, naît un univers et celui-ci définit une unité. La description, l’invention et le maniement d’unités sont à la base de toute recherche scientifique.

FIN!

…………………………………………………………………………………………………………

Tout ceci pourrait se réduire (dans un esprit de synthèse de la synthèse) à :

440 * 2 ^ (0.999/1000) ≈ 440.304785287 = 1 cents, ce qui revient à 440 * 2 ^ (1/1200)

Visites conseillées

http://www.sengpielaudio.com/calculator-centsratio.htm

http://hyperphysics.phy-astr.gsu.edu/hbase/Music/cents.html#c1