Divertimenti & Heurística aritmética
aplicables al empleo de los diferentes diapasones
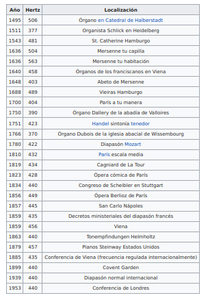
Estudio de caso
S = abreviación de savart
432 Hz
Hercios (Hz) – cents (∆) – savarts (s)
(f2 – f1 = f0 Hz) × 4Ks= ∆
4 s = 1 Hz
4∆ = 1s
Verificación : (f2 ÷ f1 ) × Diapasón modificado = Diapasón estándar
2^(12/12) × 432 = 864 Hz [A5 de 432 / G#5 + 68 ∆]
Diferencia
32 cents ÷ 4 = 8 savarts ( 4∆ = 1 savart)
440 – 432 = 8 Hz ~ (8s * 4 ∆)
440 ÷ 432 = 1.01851851852 PIL
1.01851851852 × 432 = 440 Hz

Corolario tautológico
S = 1000 x Log ( A / B )
(0,301 / 12) = 0.02508333333 PIL
(0.02508333333 * 1000) = 25.08333333 savarts [½ tono] → 25 (s)
Si un semitono (100 cents) es igual a 25 savarts, 100 cents entre 5 savarts será igual a 4 cents. Por consiguiente 1 savart será ~ 4 cents.
S = 1000 x Log ( A / B )
Recordatorio
100 ∆ = 25 (s)
Sea 1 (s) = 4 ∆ × 25 = 100 ∆ ~ 1 semitono
Búsqueda de la frecuencia de la nota Do [diapasón 432 Hz]
2 ^ (-9 /12) × 432 Hz = 256.868736841 Hz [C3 (-32 ∆) diapasón 432] o
[B3 + 68 cents D 440]
El diapasón: 432 (-32 cents de 440)
256.868736841 × 1.01851851852 = 261.625565301 [ C4]
Fuente: 440 ÷ 432 = 1.01851851852
Entonces:
2 ^ (9 ÷ 12 ) × 256.868736841 = 432.000000001 Hz [diapasón modificado]
256.868736841 ÷ 16 = 16.0542960526 Hz
[ C0 – 32 cents diapasón 432] o [B3 (-1) + 68 cents]
Aditivo
Otra manera aún más sintética : operación directa con los savarts
S = 1000 x Log ( A / B )
1000 × log(440 ÷ 432) = 7.96892967128 [8]
8^(1200 ÷ 1200 ) × 256.868736841 = 2054.94989473 Hz [C7 + 32∆]
Recorrido: 3600 ∆ ÷ 1200 ∆ = 3 octavas
ó
8192 ^ (1200 ÷ 1200 ) × 27 Hz = 221184Hz [A13 (-32∆)]
Recorrido 12 octavas
Ossia
sentido descedente
432 ÷ 2 ÷ 2 ÷ 2 ÷ 2 = 27 Hz [A0 – 32∆]
432 ÷ 16 = 27 Hz [A -1 (- 32∆)]
sentido ascendente
432 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 x 2 = 221184
Tesitura espacial
2^((12 / 12) × 13) x 16.0542960526 = 131516.793263 [C13 (-32) o [B13 + 68 cents]
