Despliegue Fibonacci
Distinción / modelización / formalización
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 89 / 1200)) = 12436.0367215 ∆
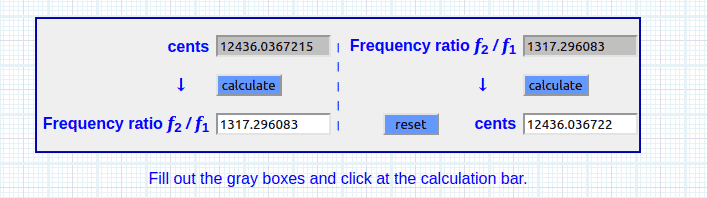
Sea, 10 octavas + 436 ∆ (una tercera mayor + 36 ∆)
Ajuste del recorrido espacial
1317.296083 × 16.352 = 21540.4255492 Hz [E10 + 36 ∆]
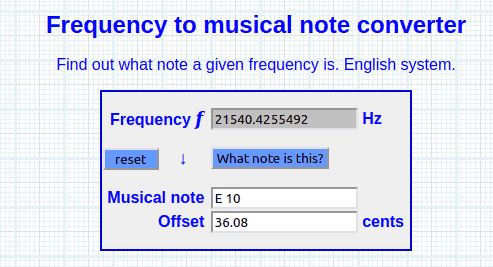
Recorrido & Ratio
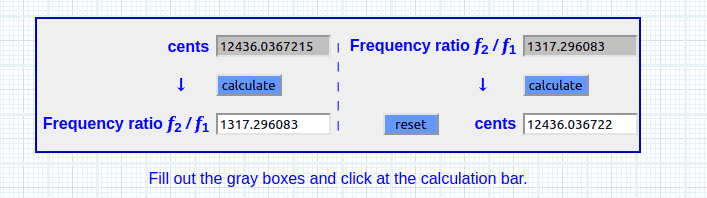
Nuestro recorrido Fibonacci en Hertz
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 0 / 1200)) * 16.352 =16.352 Hz [C0]
![]()
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 1 / 1200)) * 16.352 = 18.1793579659 Hz [C0 + 183 ∆]
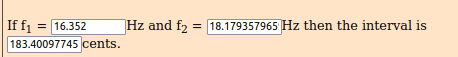
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 2 / 1200)) * 16.352 = 20.2109256392 Hz [ Eb0 + 367 ∆]
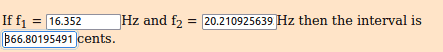
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 3 / 1200)) * 16.352 = 22.469523729 Hz [F0 + 50 ∆]
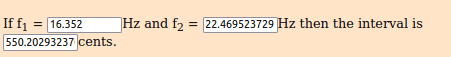
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 5 / 1200)) * 16.352 = 27.7721302125 Hz [A0 + 17 ∆]
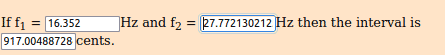
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 8 / 1200)) * 16.352 = 38.1620926379 Hz [D#1 + 67 ∆]
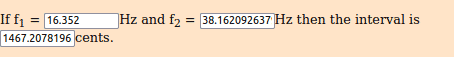
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 13 / 1200)) * 16.352 = 64.8142493836 Hz [B1 + 84 ∆ ]
![]()
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 21 / 1200)) * 16.352 = 151.262682805 Hz [D#3 + 53 ∆]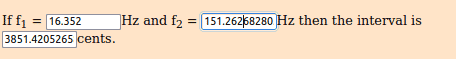
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 34 / 1200)) * 16.352 = 599.558295362 Hz [D5+ 36 ∆]
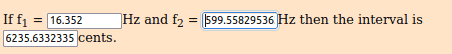
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 55 / 1200)) * 16.352 = 5546.15926215 Hz [ E8 + 87∆]
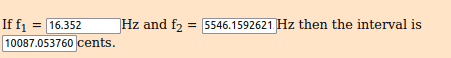
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 89 / 1200)) * 16.352 = 203354.072469 Hz [ E8 + 87 ∆]
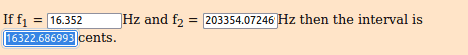
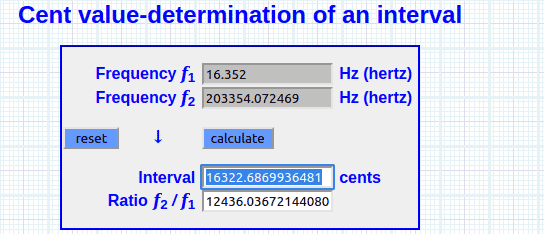
∞ …
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 144 / 1200)) * 16.352
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 233 / 1200)) * 16.352
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 377/ 1200)) * 16.352
2.41767094133 ^ (((1.618 ÷ 1.618) × 144 × 610 / 1200)) * 16.352
